Nombres complexes (équations)

Sommaire

Ce cours traite des nombres complexes dans le contexte des équations. Il recouvre et déborde, parfois de façon importante, le programme des mathématiques expertes des terminales déjà abordé dans le cours WIMS Nombres complexes (trigonométrie et géométrie) .

Pour vous assurer de vos connaissances de base sur les nombres complexes, consultez le cours WIMS Nombres complexes (introduction) et testez-vous sur les exercices. Le cours WIMS Géométrie du plan complexe décrit les isométries et les similitudes du plan complexe avec exercices et figures.

Nous commençons par un panorama des liens entre Ensembles de nombres et équations .

Mathématiques expertes

Equations du second degré

Autres équations

Racines n-ièmes d'un nombre complexe

Pour aller plus loin...

Ces chapitres supposent une certaine pratique du calcul ou permettent de l'acquérir !

Ensembles de nombres et équations

Les divers ensembles de nombres que vous connaissez sont reliés à la recherche de solutions d'une équation. Cet exposé privilégie cette approche ; il n'est pas historique mais ce tour d'horizon est instructif.

Ensemble

Au début étaient les nombres entiers naturels, désignés par des symboles appelés chiffres : 1, 2, 3..., auxquels on adjoignit ultérieurement le zéro. À ces nombres furent associées des opérations : addition et multiplication de deux entiers naturels. On obtint l’ensemble et on sait dès lors ce que signifie le nombre 4865, en écriture décimale.

Dans cet ensemble, l’équation x + 2 = 5 a une solution : x = 3. Mais l'équation x + 6 = 5 n'a pas de solution dans . Cette équation a une solution dans un ensemble qui contient .

Ensemble

Cet ensemble, nommé , est l'ensemble des entiers relatifs. Il contient et d'autres nombres : les solutions des équations qui se ramènent au type x + a = b avec et . Ces nouveaux nombres sont les opposés des entiers naturels, on les note . L'équation x + 15 = 5 a maintenant une solution dans : x = -10.

Dans , sont définies une addition et une multiplication qui prolongent celles de .

Dans , l'équation 2x+6=5 n'a pas de solution ...

Ensemble

L'ensemble des nombres rationnels contient et d'autres nombres, les solutions des équations qui se ramènent au type (où , non nul, n'est pas un multiple de ). On écrit ces nombres comme des fractions : où et sont des entiers relatifs, avec . Cette écriture est précisée par des règles d'égalité : si et seulement si .

On définit aussi des opérations, addition et multiplication dans qui prolongent celles de . Dans cet ensemble tout élément a un opposé et tout élément non nul a un inverse. En résumé, les quatre "opérations" sont possibles : addition, soustraction, multiplication et division, on dit alors que est un corps.

On démontre assez facilement que les nombres rationnels ont un développement décimal soit fini, soit périodique à partir d'un certain rang. C'est une propriété caractéristique de ... Exemples : 1,235 ou -15,235785678567856... avec une répétition infinie du bloc 7856.

L'équation x2 = 2 n'a pas de solution rationnelle. Si est un nombre positif vérifiant cette équation, nous démontrons ici qu'il n'est pas rationnel.

Ensemble

L'ensemble des nombres réels contient et d'autres nombres dits irrationnels. Parmi les nombres irrationnels, on trouve évidemment , , ... Il en existe d'autres comme par exemple, le rapport constant entre la circonférence d'un cercle et son diamètre qui est noté et dont une valeur approchée est Le développement décimal de ce nombre n'est pas périodique. Un autre exemple est le nombre e : c'est le nombre réel dont le logarithme népérien vaut 1. Une valeur approchée est

Dans , on définit aussi une addition et une multiplication qui prolongent celles de .

Mais dans , l’équation x2 = -1 n'a pas de solution.

Ensemble

Nous finissons notre tour d'horizon des ensembles par l'ensemble des nombres complexes. Historiquement, l’idée des nombres complexes est apparue pour aider à la résolution des équations de degré trois (voir cette page ). On a défini un nombre noté qui, par définition, est une solution de l’équation x2 = -1 et vérifie donc l'égalité .

Avec et les nombres réels, grâce aux opérations prolongeant celles de , on construit de nouveaux nombres ( ) qui forment l'ensemble .

Cet ensemble a de nombreuses propriétés algébriques et géométriques vues dans ce cours et les précédents.

Racines carrées d'un nombre complexe

Soit u un nombre complexe non nul. On cherche les nombres complexes z vérifiant z2 = u.

Propriété. Soit . L'équation z2 = u admet toujours deux solutions (opposées) : les racines carrées de u.
Démonstration avec l'écriture algébrique. Posons et .

À ces deux égalités, on adjoint souvent une troisième, qui facilite la résolution. Elle porte sur l'égalité des modules de z2 et u : .
On obtient les trois égalités :
Des première et troisième équations, on déduit une solution pour x2 (par exemple), puis, en prenant les racines carrées, deux valeurs pour x : x1 et -x1 . En reportant ces valeurs de x trouvées dans la seconde équation 2x y =b, on obtient les valeurs correspondantes pour y : et . L'ensemble des solutions cherchées de z2 = u est donc :

.

Pour achever la démonstration, on vérifie que la troisième égalité est bien satisfaite, ce qui est le cas.

Démonstration avec l'écriture exponentielle. Soit u un nombre complexe non nul. Il existe tel que . On cherche les nombres complexes avec vérifiant z2=u.

On obtient donc deux solutions : et . Comme vaut -1, on a bien deux solutions opposées.
Exemples. 1. Avec l'écriture algébrique, calculer les racines de . Il s'agit de résoudre le système :

On en déduit 2x2 = 8, donc et les valeurs correspondantes pour y : . Les deux racines de sont et .

2. Avec l'écriture exponentielle, calculer les racines de . On peut écrire : . En appliquant ce qui a été dit plus haut, on obtient : et .

3. Exemple à données aléatoires

Dans les exercices, on choisira la méthode adaptée à la forme des données.

Exercice. Racine carrée
Exercice. Calculer les racines carrées de , de , et de .
Solution. On obtient :
et
et
et
Exercice.

Calculer avec l'écriture algébrique, puis avec l'écriture trigonométrique, les racines carrées de . En déduire les valeurs de et de .

Solution.
  • Si l'on note , alors on peut écrire :
    On en déduit facilement les deux racines carrées :
    et

  • On obtient ainsi les deux racines carrées. et
  • Par , on sait que les sinus et cosinus de sont positifs.
    Par , on sait que les sinus et cosinus de sont négatifs.
    On trouve donc : et

Exemple à données aléatoires

On désire trouver la racine carrée d'un nombre complexe donné de manière algébrique, par exemple c = -4 -2i . On cherche donc un nombre complexe z = x + i y tel que z2 = -4 -2i avec x et y appartenant à
  1. On écrit ce que signifie l'équation z2 = c en termes de x et de y.
    Comme z2 = (x2-y2) + 2i x y, l'équation est équivalente au système d'équations

    On peut a priori résoudre à partir de ces deux équations. Mais on va en utiliser une autre qui va simplifier la résolution
  2. On traduit donc le fait que ce qui donne


  3. Et quand on a la valeur de x2 + y2 et celle de x2 - y2, que voulez-vous faire d'autre que d'en déduire la valeur de x2 et de y2 en ajoutant et retranchant ces deux équations ?

    Au fait, voyez-vous une raison a priori pour que ces valeurs soient positives ?
  4. Quelle condition n'a-t-on pas utilisée ? 2x y = -2. Ainsi x et y sont de signe contraire. On a donc et avec une contrainte sur les signes pm.
Les solutions sont

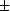et en approchant et .

Équations du second degré à coefficients réels

Il s'agit d'un cas particulier important de l'étude générale qui sera reprise à la page suivante.

Avant de résoudre une équation du second degré dans , révisez la résolution de l'équation du second degré à coefficients réels dans le cours Trinôme du second degré , et en particulier la mise sous forme canonique. La résolution des équations du second degré dans suit exactement la même démarche, ce qui conduit à calculer la racine carrée du discriminant et, dans , c'est toujours possible.

Propriété.

Si a,b,c sont réels, alors est un réel positif ou négatif.
1. Si est positif ou nul, on est ramené à l'équation du second degré connue, dont on connaît les solutions.
2. Si est négatif, puisque l'on résout maintenant dans , on peut poser avec , et les deux racines de , c'est-à-dire les nombres dont le carré vaut , sont .
L’équation, dans ce cas particulier où les coefficients sont réels, admet ainsi deux racines complexes conjuguées :

et

Leurs images dans le plan complexe sont symétriques par rapport à l'axe réel.
Attention, cette dernière propriété géométrique n'est pas vraie dans le cas général où a,b,c sont complexes.
Exemple. On demande de résoudre l'équation 4z2-24z+45=0.
Le discriminant vaut Les solutions de l'équation sont donc : . L’ensemble des solutions est donc . Elles sont représentées dans le dessin ci-dessous.

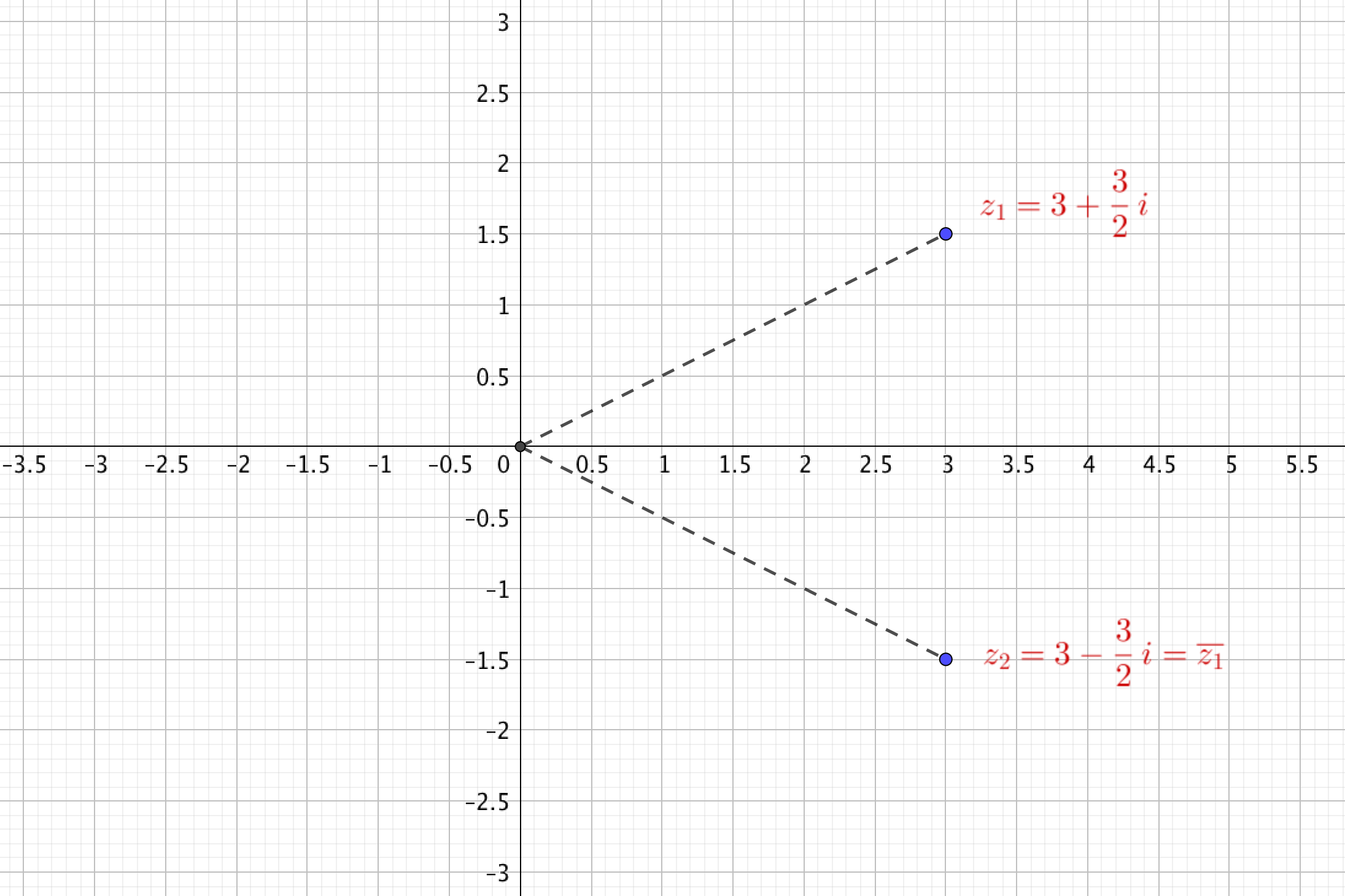
figure

Exercices. Trouver les solutions des équations suivantes :
1. z2-4z+8=0
2. z2+8z+41=0
3. -12z2+48z-75=0

Solutions
1.
2.
3.

Équations du second degré dans C

Dans le prolongement de la page précédente, nous traitons ici de la résolution des équations du second degré à coefficients complexes. La résolution dans suit exactement la même démarche, ce qui conduit à calculer une racine carrée du discriminant qui peut être un nombre complexe quelconque et, là encore, c'est toujours possible.

Propriété. Soient a, b, c des nombres complexes avec . L'équation du second degré a z2+b z+c=0, de la variable complexe z, admet dans deux solutions distinctes ou confondues : et , où est l'une quelconque des deux racines carrées du discriminant , c'est-à-dire vérifiant :
Exemple à données aléatoires.
Exercice I. Résoudre dans les équations :
  1. .

    Solution et .

  2. .

    Solution et .

  3. .

    Solution et .

Exercice II.

1. Résoudre dans l' équation .

Aide. Le but est de se ramener à une équation du second degré. La symétrie des coefficients 1,-4,2,-4,1 conduit à utiliser une méthode particulière. Après avoir remarqué que z=0 n'est pas solution de l'équation, on pose . En élevant au carré, cela donne .
Comme 0 n'est pas solution de l’équation, on divise les deux membres de l'équation par z2, et on regroupe judicieusement...
On arrive à l'équation : (*) . On calcule .
On obtient deux solutions de l'équation (*), Z1 et Z2. il ne reste plus qu'à résoudre les deux dernières équations et
Solution. L'ensemble des solutions est :

2. Résoudre dans l'équation où u est un nombre complexe donné non nul. Montrer que les racines de cette équation sont les affixes des sommets d'un triangle rectangle isocèle.

Une des racines est facile à trouver : le problème se ramène donc rapidement à une équation du second degré que vous savez résoudre !
Solution. L'équation admet trois racines . Appelons O A B le triangle dont les affixes des sommets sont les trois racines, en choisissant que O a pour affixe 0, A a pour affixe u et B a pour affixe . Si on écrit en complexe l'affixe de u : , alors . On voit que l'argument de est l'argument de u augmenté de autrement dit l'angle est un angle droit. Comme u et ont le même module , finalement le triangle A O B est un triangle rectangle isocèle.

Exemple à données aléatoires.

Exemple à données aléatoires. Résolvons l'équation

() z2 + () z+ = 0

Le discriminant est . On calcule les racines carrées de 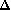Delta par la méthode algébrique : d ou -d. Les racines de l'équation sont alors et

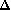En particulier, comme dans le cas réel, l'équation a une racine "double" lorsque le discriminant Delta est nul.

Exercices sur les racines d'un trinôme de degré 2

Le résultat suivant, déjà énoncé dans le cas de la résolution dans (voir cette page ), peut être utile dans certains cas et souvent pour une vérification des solutions.

Relations entre racines et coefficients d'un trinôme du second degré. On considère l'équation du second degré à coefficients complexes a z2+b z+c=0, avec . On sait qu'elle admet toujours deux solutions, distinctes ou confondues, z1 et z2. Leur somme et leur produit vérifient :

et .


Exercices.
  1. Racines d'un polynôme quadratique.
  2. Exercices sur les racines doubles.
  3. Lien entre racines et coefficients.
  4. Que peut-on dire de la différence des racines ?
    Solution. On se place dans le cas où p est imaginaire pur, et q réel. L'autre cas de l'exercice (il y en a deux) se traite de façon analogue.
    Soit et . L'hypothèse voulant que z1 et z2 ne soient ni réels ni imaginaires purs, cela revient à dire qu'aucun des termes a1, a2, b1, b2 n'est nul. 1- La somme des racines vaut -p. Donc .
    Puisque -p est imaginaire pur, a1 + a2=0.
    D'où : et 2- Le produit des racines vaut q. Donc . Il est réel donc b2- b1=0 Et et .
    Donc z1 - z2 = 2a1 est réel.
Exercice. Ici, vous devez trouver le polynôme de degré 2 dont les racines sont dessinées : le polynôme à trouver est à coefficients complexes ou à coefficients réels

Exercice. Exercices sur les racines doubles.

Polynômes

Rappels et définitions.
  1. Soient des nombres réels ou complexes (les coefficients) avec , et z une variable réelle ou complexe. Un polynôme P est une somme algébrique finie de la forme : .
  2. Le degré d'un polynôme non nul est l'entier naturel n.
  3. Une fonction polynôme est une fonction f de dans , qui à .
  4. On appelle racine d'un polynôme, toute valeur z qui annule la fonction polynôme f, toute solution de l'équation f(z)=0.
  5. L'ensemble des polynômes à coefficients réels est noté , le sous-ensemble-ensemble des polynômes de degré n est noté , l'ensemble des polynômes à coefficients complexes est noté .

Remarque. Dans la pratique, on notera un polynôme soit par une lettre majuscule P, soit sous la forme P(z) ou P(x) pour indiquer le nom de la variable, sans pour autant le confondre avec la fonction polynôme.

Propriété : racines conjuguées d'un polynôme à coefficients réels.
Soit P un polynôme de . Si z0 est une racine de P, alors est une autre racine de P.
Démonstration. Soit un polynôme quelconque à coefficients réels. Si z0 est une racine de P, on a : P(z0)=0. Ceci est équivalent à qui s'écrit :
. En utilisant les propriétés des conjugués et le fait que tous les coefficients ai sont réels, c'est-à-dire pour tous les indices, On en déduit . Donc qui annule P est aussi une racine de P.

On rappelle une identité remarquable très utile dans ce chapitre (vérifiez-la !) :

Identité remarquable. Soit a et z des nombres complexes.

Exemple. z3-27 = (z-3)(z2+3z+9)
Exercice. Factoriser z5+32 en utilisant l'identité remarquable.

Solution

z5+32 = (z+2)( z4 -2z3 +4z2 -8z +16)

Factorisation d'un polynôme

Théorème. Soit a un nombre complexe et , avec ( ), un polynôme à coefficients complexes et de la variable complexe z . Si P s'annule en a, alors P se factorise par z-a.
Il existe donc un polynôme vérifiant (*)

Démonstration.

Sachant que P(a) = 0, on peut écrire : .
Dans toutes les expressions (zk-ak), , on peut mettre en facteur (z-a) grâce à l' identité remarquable vue précédemment. D'où le résultat.

Remarques.

  1. Ce théorème est en fait une équivalence.
  2. En général, on trouvera Q en développant les deux membres de l'égalité (*), et en identifiant les termes de même degré. Voir pages suivantes.
  3. Si P est un polynôme de , Q est aussi un polynôme de . Ceci découle facilement de la démonstration ci-dessus.
Définitions.

Soit P= (z-a) Q. Si Q s'annule pour la valeur a, on dit que a est une racine double (au moins) de P et il existe tel que Q=(z-a) S, et P s'écrit : P= (z-a)2 S.

S'il existe un entier naturel p, non nul, et un polynôme P1 de tel que P= (z-a)p P1 avec , on dit que P admet a pour racine d'ordre p et que p est l'ordre de multiplicité de la racine a.

Factorisation des polynômes à coefficients réels

Factorisation d'un polynôme de degré 2.

Soit P2 un polynôme de degré 2 de (à coefficients réels) : P2= a2 z2+ a1 z + a0 avec . On a vu ici que P2 a deux racines z1 et z2, éventuellement confondues, dans .
Exercice. Soit un polynôme de sans racines réelles. Donner son écriture en fonction du module et de l'argument de la racine z1.
Solution. Notons : d'où . On en déduit :

Exercice. Racines conjuguées
Écrire les racines sous forme algébrique .

Factorisation d'un polynôme de degré 3.

Soit P3 un polynôme de degré 3 à coefficients réels : P3 = a3 z3 + a2 z2 +a1 z +a0 avec .
Propriété. La fonction polynôme de variable réelle, à coefficients réels de degré 3, définie sur par : f(x)= a3 x3 + a2 x2 +a1 x +a0 (et de façon générale toute fonction polynôme de degré impair) s'annule toujours au moins une fois sur . Le polynôme associé admet donc une racine réelle que l'on peut noter , et se factorise avec un facteur
La fonction (continue) se comportant à l'infini comme son terme de plus haut degré (en x3) tend vers en , et vers en . Le théorème des valeurs intermédiaires assure donc qu'elle s'annule au moins une fois.

Soit P3 un polynôme de degré 3 à coefficients réels. D'après la propriété, on peut trouver, d'une façon ou d'une autre, une racine réelle de P3 pour le factoriser. En effet, d’après le théorème de factorisation (voir ici ), il existe tels que P se factorise sous la forme : . Posons Q = a3 x2 + a4 x +a5
On détermine Q en développant les deux membres, puis en identifiant les termes de même degré, en vertu de l'unicité de l'écriture d'un polynôme. Il ne reste plus qu'à factoriser ce polynôme de degré 2 comme on l'a fait plus haut.


Exemple. Pour factoriser le polynôme P= x3-x2-4x + 4 = 0, on constate que x=1 est une racine de P. Le polynôme se factorise donc sous la forme P= (x-1)(a x2+b x+c). On développe le membre de droite et on regroupe les termes de même degré. P= a x3 + (b-a) x2 + (c-b) x -c. On sait que l'écriture d'une polynôme est unique, ce qui conduit à identifier les coefficients de même degré.

Ceci est équivalent à a=1, b =0 et c = -4 et on obtient P(x)= (x-1)(x2-4) =(x-1)(x-2)(x+2).
Exercices.

A. Factoriser les polynômes suivants dans (on commencera pas trouver, en faisant des essais, une racine réelle simple...).

Solution.
  • P1(x) = x3-4x2 -7x +10 =(x-5)(x-1)(x+2).
  • P2(x)=6x3+11x2-3x-2 = (x+2)(2x-1)(3x+1).
  • P3(x)=x3-x2-x-2 = (x-2)(x2+x+1).

B. Factorisation

Factorisation dans C[X]

Jean Le Rond d'Alembert est le premier à avoir énoncé, sous une forme complète, le théorème fondamental de l'algèbre, souvent nommé simplement de d'Alembert, déjà avancé par Viète et Girard mais qui n'arrivèrent pas à le démontrer de façon précise. (Tiré de ChronoMath )

Théorème fondamental de l'algèbre : le théorème de d'Alembert. Un polynôme non constant de admet au moins une racine complexe.
Corollaire. Un polynôme P de degré n admet, dans , exactement n racines, distinctes ou confondues. On peut écrire où k est un nombre complexe.

Le théorème de d'Alembert permet de dire que, si Pn est un polynôme non constant de degré n, il existe un nombre complexe z1 racine de Pn et un polynome de degré n-1, tels que . On applique à répétition le théorème de d’Alembert (démonstration par récurrence) :

le polynôme est de degré 1 et de la forme , avec a,b complexes, a non nul.
On met en valeur la racine de P1 : , d'où

.

On a ainsi mis en évidence les n racines du polynôme , distinctes ou confondues.
Exemples.

,

On trouvera une liste d’exercices dans la page suivante.

Exercices sur factorisation et équations polynomiales

I. Factorisation avec une racine suggérée.

1. Sachant que est racine du polynôme P(X) = X4-2X3+6X2+22X+13, factoriser ce polynôme dans .

Solution. , ainsi que , puisque le polynôme est à coefficients réels, sont des racines de P. Celui-ci, dans sa factorisation, admet donc le facteur .
Il existe donc un polynôme Q tel que . Q est un polynôme de degré 2, que l'on détermine facilement en développant les deux membres, comme dans l'exemple ci-dessus, et en identifiant les termes de même degré. On trouve Q = X2+2X+1 =(X+1)2. La factorisation de P dans est : P=(X2-4X+13)(X+1)2

2. Trouver toutes les solutions dans de l'équation E : , sachant qu'elle admet une solution réelle.

Solution. Soit x cette solution réelle. Si elle est solution, alors (implication) la partie imaginaire de est nulle, c'est-à-dire x vérifie 2x2-5x+2=0, équation qui admet deux solutions et x = 2.

Il reste à regarder quelles valeurs satisfont l'équation donnée (on a raisonné par implication). Seule x=2 convient et on peut, dès lors, factoriser par (z-2).

En identifiant les termes de même degré, on arrive à b2 =1, b1= -1+2i, b0= -3-i. L'équation E devient : . L'équation de degré deux admet pour solutions : et .

Les solutions de E sont : 2, et .

3. Factoriser le polynôme :

Chercher une racine réelle.
Solution.

4. On cherchera une racine imaginaire pure des polynômes suivants, puis on les factorisera :

Si une racine est imaginaire pure, alors elle est de la forme où b est un nombre réel. On remplace dans l'équation, on arrive à un nombre complexe qui doit être nul (dont les parties réelles et imaginaires doivent être nulles).

.

Solution.

.

Solution.
  • La solution imaginaire pure est .
  • Le polynôme se factorise en . Les racines du polynôme de degré deux sont et
    .

Solution.

5. Résoudre dans l'équation z4 - 6z3 + 14z2 -24z + 40 = 0 sachant qu'elle admet deux solutions imaginaires pures.

On cherche des solutions de la forme où x est réel. On remplace dans l'équation, et on sépare parties réelles et parties imaginaires. Cela donne deux équations à résoudre...
Solution. Deux solutions imaginaires pures et .
Avec un peu de travail on arrive à la factorisation par ci-dessous :
z4 - 6z3 + 14z2 -24z + 40 = (z2+4)(z2-6z+10).
Les 4 solutions sont , , et .
Exercice II.

Soit le polynôme :

  1. Trouver une racine z2 de P(z) de la forme , où a est un réel à déterminer. En déduire une factorisation de P en un produit d'un polynôme de degré un et d'un polynôme de degré deux, dont on cherchera les racines. Mettre les trois racines sous forme exponentielle.
  2. Montrer que les deux suites z1,z2,z3 et z3,z2,z1 sont des suites géométriques dont on donnera la raison.
Solution.
  1. Les racines sont , et . Les formes exponentielles sont :
  2. La première suite a pour raison , la seconde .
Exercice III.

Soit P= x7 +x6 +x5 +x4 +x3 +x2 +x + 1

  1. Factoriser P dans .
  2. Factoriser P dans .
Solution.
P est la somme de 8 termes de la suite géométrique de premier terme 1 et de raison x. Puisque 1 n'est visiblement pas solution de l'équation, on peut écrire : .
Les racines de P vérifient : .
On en déduit la factorisation de P dans :

À partir de celle-ci, on obtient la factorisation dans en regroupant deux par deux les racines conjuguées (voir Exercice 2 ci-dessus) :
On trouvera une autre liste d’exercices dans la page suivante.

Équations en z et en conjugué de z

Exercice I : Équations avec modules
Exercice II : Soit Montrer que si , alors appartient aussi à D.
Solution. En passant par exemple par la forme algébrique, il est facile de vérifier que : . Par ailleurs, .
. D'où le résultat.
Exercice III : Résoudre l'équation
Solution.

Écrivons le problème avec la forme algébrique :

On écrit l'égalité des parties réelles et imaginaires :

La dernière égalité 4a3 b - 4a b3=4a b ( a +b)(a -b)=0 fournit 4 possibilités pour les valeurs de a que l'on reporte dans la première égalité pour avoir les valeurs de b correspondantes :
1. a=0 qui conduit à b=0
2. b=0 qui conduit à
3. a=b qui conduit à
4. a= -b qui conduit à
L'ensemble des solutions est : .
Exercice IV : Trouver tous les nombres complexes z vérifiant l'égalité : pour . On discutera suivant les valeurs de n.
Solution.
  1. Si n=0, on résout , soit et donc . Les solutions sont les affixes des points du cercle de centre O et de rayon 1.
  2. Si n=1, on résout . Une seule solution z=1.
  3. Si n=2, on résout . Tous les réels sont solutions.
  4. Si , on résout . Cette égalité implique (nécessité d'une réciproque) : . Ce qui conduit à : .
    Donc :
    1. soit .
    2. soit qui est équivalent à .
    Dans ce dernier cas, on a simultanément les deux égalités et , ce qui implique zn = 1. On obtient ainsi les n racines n-ièmes de l'unité. Sont-elles toutes solutions ?
    Réciproquement : Soit une racine quelconque de l'unité, avec .
    1.
    2.
    Toutes les n racines n-ièmes de l'unité conviennent donc.
    Conclusion : Si , les solutions sont z=0 et les racines n-ièmes de l'unité.
Exercice V : Résoudre les équations :
Solution.
  1. Solution de la première équation :
  2. Solution de la deuxième équation :

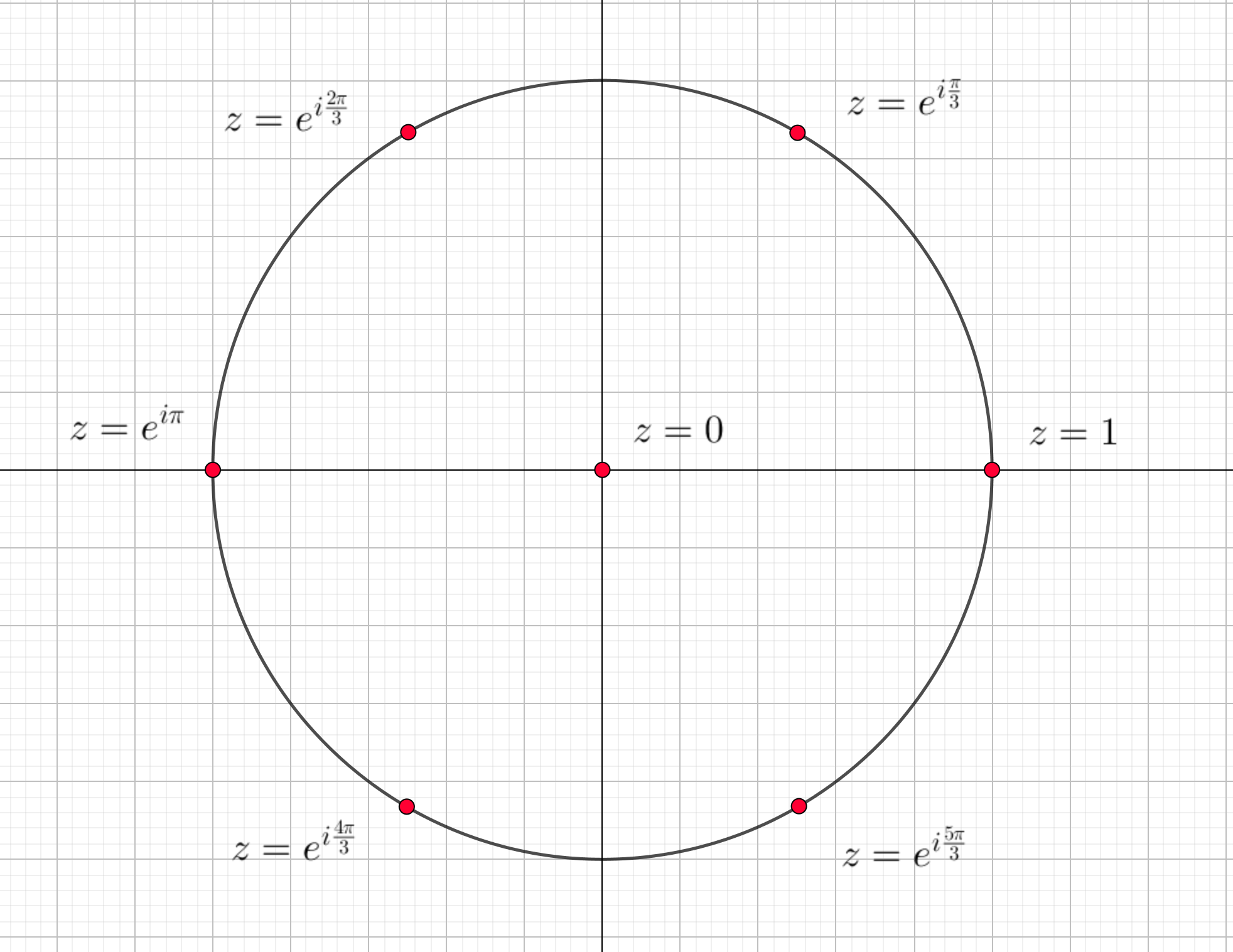
Racines n-ièmes de l'unité

Définition. Soit n entier naturel strictement positif. On appelle racine n-ième de l'unité toute solution dans de l'équation zn=1.
Propriétés algébriques.

L'équation zn=1 admet, dans , n solutions distinctes qui s'écrivent :

où k est un entier prenant n valeurs consécutives, par exemple

On note l'ensemble des racines n-ièmes de l'unité. . On peut donc factoriser le polynôme zn-1 dans :

La somme des n racines n-ièmes de l'unité, pour , est nulle.

Racines cubiques de l'unité. L'ensemble des racines cubiques de l'unité est donc noté .
. On note , donc

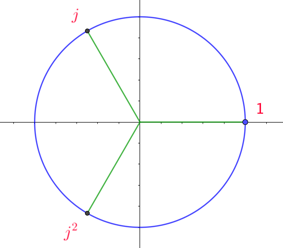
figure

Exercices.

I. Démontrer les résultats suivants : .

2. Résoudre l'équation :

Solution. z=0 est une solution évidente. Supposons par la suite que .
  • Écrivons alors le nombre complexe z sous la forme exponentielle, , avec réel quelconque. L'équation s'écrit alors :
  • Égalité des modules. donc (déja vu) ou
  • si on peut écrire : . Les solutions sont les racines sixième de l'unité, et on a raisonné par équivalence.
  • Conclusion. L'équation a 7 solutions distinctes : z=0 et , avec .

Exercices.

I. Dans , on a vu que vaut . Montrer l'égalité , puis

II. Soit , avec , l'une quelconque des n-1 racines n-ièmes de l'unité (différente de 1, puisque p est supposé non nul). Montrer l'égalité :

Solution. Il s'agit de calculer la somme de n termes d'une suite géométrique de premier terme 1 et de raison . Donc Comme , cela démontre le résultat. On retrouvera ce résultat grâce aux formules de Viète.

Exercices.
  1. Sur les racines cubiques de l'unité
  2. Sur les racines cinquièmes de l'unité
  3. Sur la somme des racines de l'unité (on pourra utiliser l'identité remarquable vue à cette page .)

Racines cubiques d'un nombre complexe

Propriété. Tout nombre complexe u non nul admet trois racines cubiques complexes, c'est-à-dire qu'il existe trois nombres complexes distincts z1, z2 et z3 tels que z13=z23=z33=u

Démonstration.

Si l'on écrit u sous forme exponentielle ( r>0) , on cherche ( ) vérifiant z3=u, c'est-à-dire . Cette condition nécessaire et suffisante s'écrit en système de cette façon :

La résolution du système donne : et (avec ), on obtient donc trois racines cubiques distinctes :

Remarque géométrique.

Si, dans le plan complexe, on considère les trois points M1, M2 ,M3 d'affixes respectives z1, z2 ,z3, puisqu'elles ont le même module, les trois points sont sur le cercle de centre O et de rayon .

Les angles sont égaux, et égaux à . Le triangle M1 M2 M3 est donc un triangle équilatéral (voir Racines n-ièmes de l'unité et polygones ).

Ci-dessous un exemple avec et ses racines cubiques.

figure

Exercices.
  1. Montrer que les racines cubiques d'un nombre complexe s'expriment avec l'une d'entre elles, et le nombre complexe .
    On sait que et que .
    Donc

  2. Placer les racines cubiques dans le plan complexe.
  3. Sur les racines cubiques

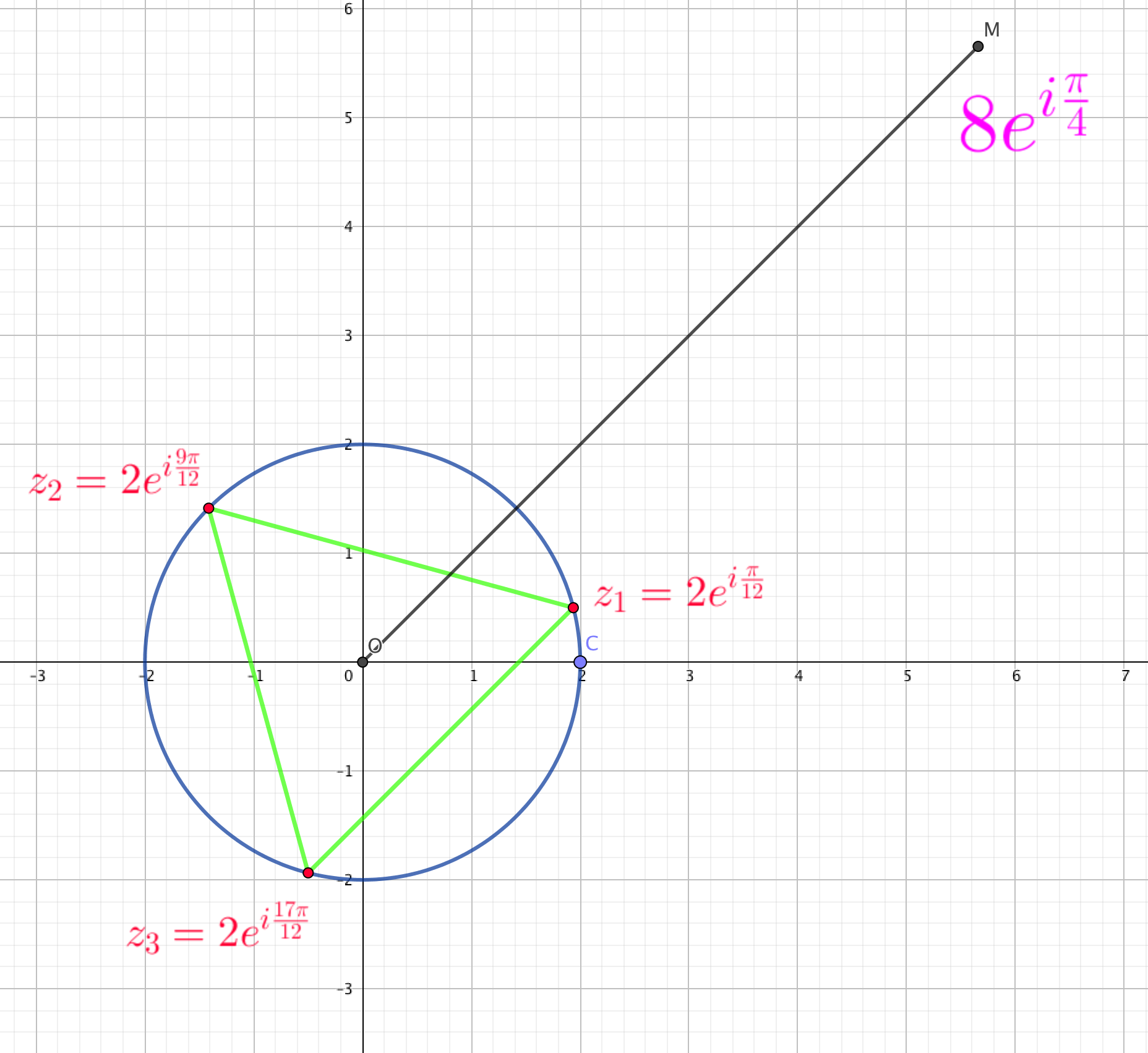
Racines n-ièmes d'un nombre complexe

Définition. Soit ( et réels, ) un nombre complexe non nul. L'équation zn=a admet n solutions distinctes appelées racines n-ièmes de a. Elles sont notées ici zk où k est un entier vérifiant :


l'entier k prenant les n valeurs consécutives comprises entre 0 et n-1.

Propriété. Si l'on sait calculer une des racines n-ièmes de a, notée par exemple , alors on les obtient toutes en multipliant par les n racines n-ièmes de l'unité . En d'autres termes, si l'on note l'ensemble des n racines n-ièmes de a, on peut écrire : .
Exercice I.

1. Calculer les racines cinquièmes de .

On trouve 5 solutions : avec

2. Calculer les racines quatrièmes de .

On trouve 4 solutions : {}
Exercice II.
  1. Soit un réel dans [ ]. Calculer, suivant les valeurs de , le module et l'argument de
    Si , alors
    Si , alors
  2. Résoudre dans , pour dans [ ], l'équation
    On trouve:
Exercice III.
  1. Quel est le degré du polynôme
  2. Soit , Résoudre l'équation P(z)= 0, et compter le nombre de solutions.

Le polynôme P(z) est de degré 2n -1 ce que l'on vérifie facilement avec la formule du binôme de Newton.


L'identité permet la factorisation :

  • Pour n =1, l'équation a une seule solution : . Cette solution reste d’ailleurs valable pour tout , du fait de la factorisation indiquée dans l'aide. Notons de plus que est une racine de multiplicité d'ordre n de P.
  • Supposons et cherchons les solutions autres que . Comme le degré de P est 2n-1, il en reste n-1 à trouver : .
    Pour , l'équation est équivalente à soit . Pour chacune des solutions, par exemple zk, le nombre est donc une racine n-ième de l'unité . On a vu que les racines n-ième de l'unité sont avec . Ici k est différent de 0 car ne vaut jamais 1. L'égalité est donc équivalente à ( découle de ).
    Par la méthode vue au chapitre "Somme d'exponentielles complexes" (dans le cours "Nombres complexes (trigonométrie et géométrie)"), on arrive à : pour . On vérifiera que le dénominateur est toujours non nul.
    Conclusion : Pour , on obtient
  • est, on l'a vu, une racine d'ordre n, on a obtenu ci-dessus n-1 racines supplémentaires, on a bien les 2n-1 (le degré du polynôme) racines distinctes ou confondues annoncées par le théorème de d'Alembert.
Exercice IV.
  1. Résoudre dans l'équation z4+1=0, puis factoriser le polynôme P= z4+1 dans
  2. Vérifier que . Représenter les racines de P dans le plan complexe.
  3. En déduire une factorisation dans (avec des coefficients uniquement réels).
.
Solution.

  1. Les racines carrées de sont (on le vérifiera) et .
    Celles de sont (on le vérifiera) et

    On en déduit la factorisation de P dans :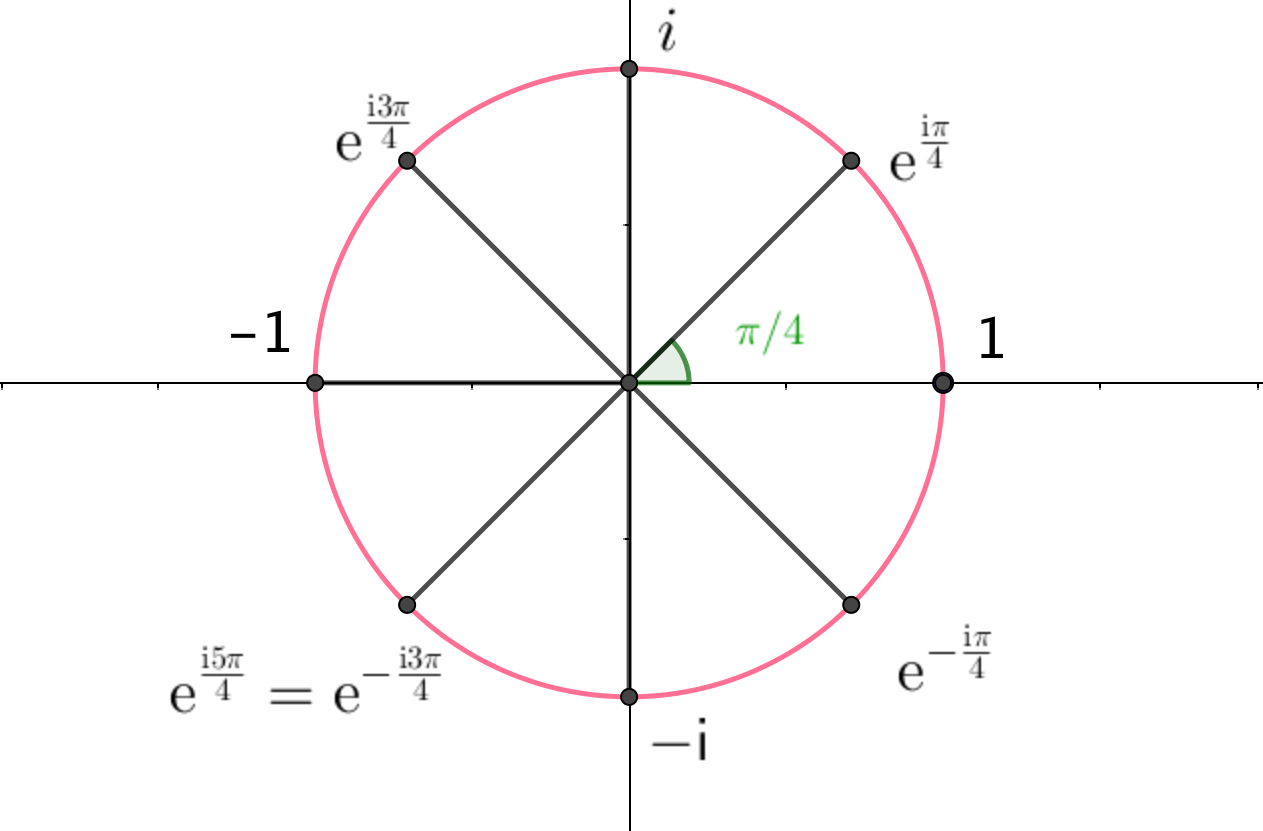
  2. .
  3. Dans l'expression de P trouvée à la première question on regroupe les facteurs 1 et 4, puis 2 et 3, et on applique le résultat de la deuxième question.

Racines n-ièmes de l'unité et polygones

Consultez ce cours DOC Polygones convexes réguliers pour des rappels sur les polygones convexes réguliers.
On utilise ici la caractérisation suivante : Un polygone convexe est régulier si ses sommets sont sur un cercle et ses angles au centre égaux.

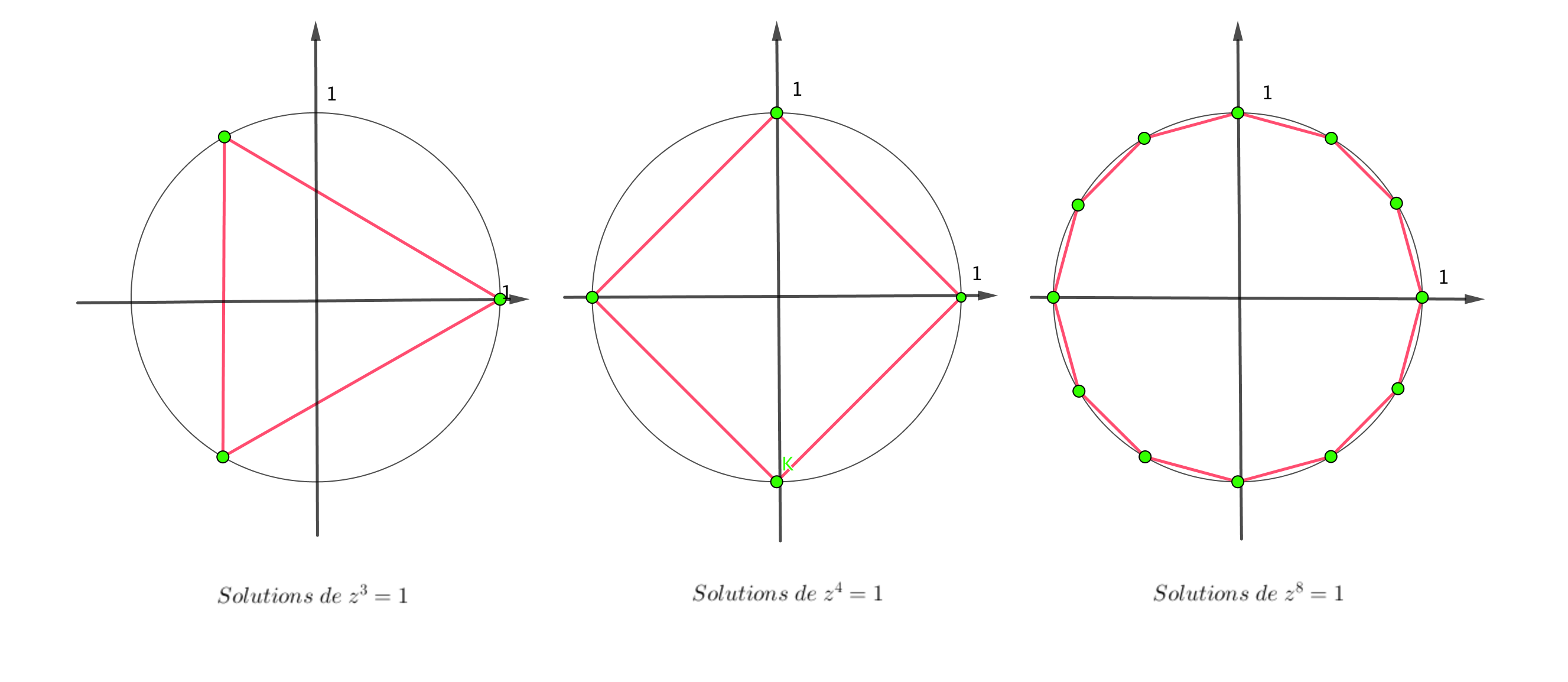
Propriétés géométriques. Dans le plan complexe, les n racines n-ièmes de l'unité sont les affixes des sommets d'un polygone régulier à n côtés dont l'un des sommets est le point d'affixe 1.

Illustration.

Pour n = 2,voici les racines n-ièmes de l'unité dans le plan complexe ; avec . vous pouvez changer aléatoirement la valeur de n ou la choisir vous-même (inférieure à 50) dans cette case :

Ensuite, et interprétez ce que vous remarquez.

n = 2
Exercice. Placer les racines quatrièmes ou cinquièmes d'un nombre dans le plan complexe.

Construction du pentagone régulier

Rappels : Polygones réguliers , construction à la règle et au compas
Exercice. Dans le plan complexe, on considère le pentagone régulier dont les sommets sont les images des racines cinquièmes de l'unité (les solutions de l'équation z5-1=0). On vérifiera au passage les égalités figurant dans l'ensemble.

{ 1, , , , }.

  1. Montrer que , , et sont les racines du polynôme P(z)= z4+z3+z2+z+1.

    Utiliser l'identité : z5 - 1 = (z-1)(z4 + z3 + z2 + z + 1)

  2. On pose et . Montrer, en calculant leur somme et leur produit (voir Relations entre coefficients et racines ), que A et B sont les racines du polynôme t2 + t - 1. Calculer A et B.
  3. En déduire les valeurs de et .
  4. On trace le cercle de centre d'affixe passant par le point D d'affixe . Montrer que coupe l'axe des réels aux points d'abscisse et . On utilisera l' équation complexe d'un cercle.

    On rappelle que le cercle de centre , d'affixe et de rayon r est l'ensemble des points d'affixe , avec

  5. En déduire une construction du pentagone régulier à la règle et au compas. Faites-la avec le module Règles et compas .
  1. Les éléments de sont les solutions de l'équation z5-1=0 ; or on a : z5-1=(z-1)(z4+z3+z2+z+1) ; les racines de P(z)=z4+z3+z2+z+1 sont les éléments de différents de 1.
  2. Le nombre A + B vaut , donc -1 puisque est racine du polynôme P.
    De , on tire
    Le polynôme du second degré en t dont la somme des racines vaut -1 et le produit des racines vaut aussi -1 est bien : t2 + t - 1. Ses racines valent et .
    On note que la première est positive et la seconde négative. Laquelle est A, et laquelle est B ?
    qui est positif du fait de la double inégalité On en déduit : et .
  3. Les valeurs des deux cosinus résultent de la question 2 : et
  4. Le rayon du cercle est . L'équation du cercle est : (). L'intersection de avec l'axe de abscisses est réalisée pour et . Ce sont donc les points d'affixe et
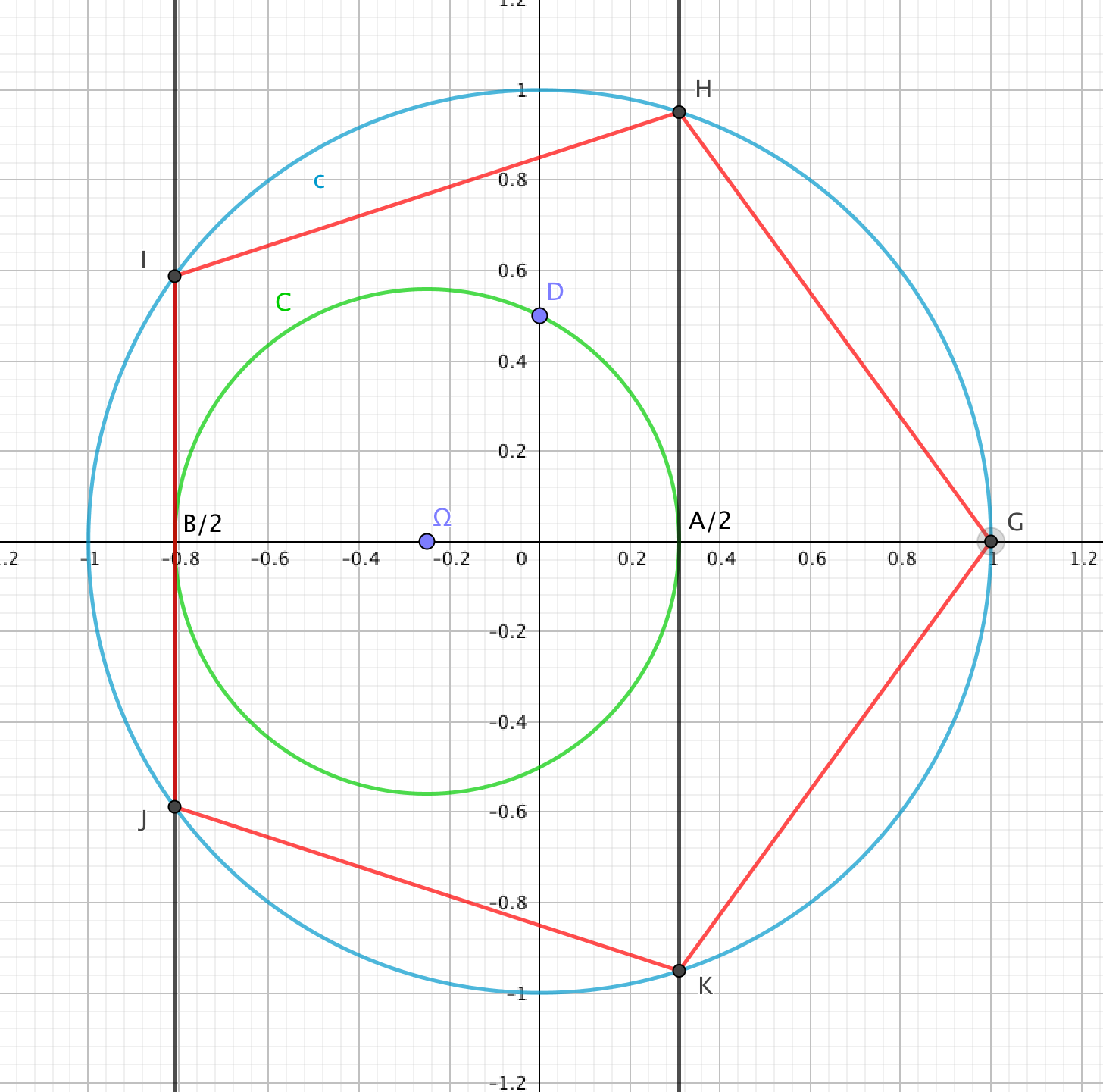
  5. On commence par tracer le cercle trigonométrique de centre O et le point G de coordonnées (1,0). On trace ensuite le cercle défini dans l'énoncé (en vert sur la figure ci-dessous) qui coupe l'axe des abscisses (on l'a vu) en et .
    On trace ensuite la perpendiculaire à (O G) au point d'affixe qui recoupe le cercle trigonométrique en deux points H et K. De , on tire l'égalité (mod ). Les points G et H sont donc les sommets du pentagone, par symétrie K également.
    On fait de même au point d'affixe et on obtient les deux derniers sommets I et J. Il ne reste plus qu'à tracer les côtés de G H I J K

figure

A cette page du cours DOC Polygones convexes réguliers , vous trouverez d'autres constructions du pentagone régulier.

Relations entre coefficients et racines

Polynôme du second degré.

Cette page, et celle qui suit, se proposent de généraliser ce résultat vu ici (assorti de techniques de vérification) :
Propriété. Si le polynôme du second degré à coefficients complexes a2 z2+a1 z + a0 ( ) admet deux racines z1 et z2 dans , alors leur somme et leur produit s'expriment de façon simple en fonction des coefficients :

Démonstration. Le polynôme factorisé avec les deux racines z1 et z2 dans , s'écrit et se développe sous la forme : .
En identifiant les deux dernières écritures, on obtient le résultat annoncé.

Remarque. On a vu dans le premier exercice de Factorisation des polynômes à coefficients réels qu'un polynôme de s'écrit en fonction de ses racines complexes et sous la forme : . On retrouve le fait que le produit vaut et la somme .

Ces relations permettent d'établir l'équation du second degré vérifiée par deux inconnues et d'ainsi les calculer.

Exercices.
  1. Calculer la somme et le produit des racines sans les calculer.
  2. Trouver deux nombres connaissant leur somme et leur produit
  3. Calculer la valeur de résistances

Polynôme du troisième degré.

Le polynôme P3(z) = a3 z3+a2 z2+a1 z+ a0, (*) (avec ) admet dans trois racines distinctes ou confondues z1, z2 et z3. Il se factorise donc sous la forme : P3(z) = a3(z-z1)(z-z2)(z-z3). En développant cette expression (faites le !), on obtient :

(**).

En identifiant les deux écritures (*) et (**) du polynôme (unicité de l'écriture), on obtient :

Polynôme du quatrième degré.

Exercice.
  1. Refaire le même calcul que ci-dessus avec un polynôme de degré 4.
  2. Comparer les résultats obtenus avec les résultats précédents. En regardant la forme des résultats, que peut-on conjecturer ?
Solution.
1. Ce polynôme que l'on écrira P4(z) = a4 z4 +a3 z3+a2 z2+a1 z+ a0, (*) (avec ) admet dans quatre racines distinctes ou confondues z1, z2,z3 et z4. Il se factorise donc sous la forme : P4(z) =a4(z-z1)(z-z2)(z-z3)(z-z4). En le développant (faites le !), on obtient :

(z1 z2+z1 z3 + z1 z4 + z2 z3+ z2 z4 +z3 z4) z2 (**).

En identifiant les deux écritures (*) et (**) du polynôme (unicité de l'écriture), on obtient :

2. La forme un peu particulière des résultats est indiquée ci-dessous.

Généralisation.

En regardant ces trois résultats, on commence à voir des régularités ... Dans les trois cas, on a pris les produits des racines une par une et on en a fait la somme, puis les produits deux par deux et on en a fait la somme, puis les produits trois par trois et on en a fait la somme... etc.
  1. Le dénominateur est toujours le coefficient du terme de plus haut degré.
  2. Les indices des numérateurs sont dans un ordre régulier décroissant, et on observe une alternance de signe.
On retrouvera ces propriétés pour les degrés plus élevés à la page suivante .

Formules de Viète

Soit P un polynôme de degré n, à coefficients complexes, de la variable z complexe. Il existe donc un (n+1)-uplet de complexes, coefficients de P, , avec tel que : . Ici , on a vu que ce polynôme admet, dans , n racines distinctes ou confondues : . Ces racines sont notées par des noms différents mais peuvent être égales pour certaines d?entre elles (racines doubles, triples...).

On définit maintenant de façon générale les sommes de produits de racines qu'on a vu apparaître à la page précédente .

Définition.

Soit p un entier naturel, . On appelle polynômes symétriques élémentaires les expressions notées des n variables définies par :

.

Dans le cas où les variables sont les racines d'un polynôme P, le nombre est la somme de tous les produits de p racines de P, choisies parmi les n racines, ces p racines étant choisies de toutes les manières possibles.

Exemple. Si P est un polynôme de degré 4, avec 4 racines z1, z2,z3, z4 dans , distinctes ou non, alors les polynômes symétriques des racines de P valent :
Proposition. Formules de Viète.

Les valeurs des poynômes symétriques des racines d'un polynôme s'expriment en fonction des coefficients du polynôme par les formules de Viète.

Les formules de Viète pour les petites valeurs du degré ont été démontrées à la page précédente.
Exemple. Les calculs pour un polynôme de degré 4, faits à la page précédente s'écrivent maintenant avec les formules de Viète :

Exercices d'applications des formules de Viète

Exercice I. Soit P(z) = 2z3 -4z2+7z -6. On note et les racines de ce polynôme.
  1. Calculer, sans utiliser les valeurs des racines, , puis .
  2. En utilisant que l'on exprimera de deux manières différentes, en déduire la valeur de
  • a0 = -6, a1 = 7, a2 = -4, a3 = 2
Solution.
  2. .
  3. , puisque , et sont des racines de P. Donc . Calculons-le autrement:

    On en déduit :

Polynômes symétriques

Définition. Un polynôme symétrique est un polynôme de plusieurs variables qui est invariant (inchangé) par toute permutation de ses variables.
Exemples : tous les polynômes figurant dans les exercices ci-dessous sont des polynômes symétriques.
Propriété. Un polynôme symétrique peut s'écrire comme somme de produits de polynômes symétriques élémentaires.
Exercices WIMS.
  1. Longueur de deux côtés de l'angle droit d'un triangle rectangle dont on connaît le périmètre
  2. Longueur de deux côtés de l'angle droit d'un triangle rectangle dont on connaît l'aire.
  3. Trouver deux nombres connaissant leur somme et leur produit
Exercice II. On suppose que X,Y,Z sont les racines d'un polynôme P de degré 3. On demande d'exprimer les quantités suivantes en fonction des polynômes symétriques élémentaires et .
  1. R(X,Y,Z) = X3+Y3+Z3
  2. S(X,Y,Z) = X2 Y+X Y2+X Z2+X2 Z+Y2 Z+Y Z2
  3. T(X,Y,Z) = X4+Y4+Z4

Solution. Les polynômes R, S et T sont symétriques en X, Y et Z.
Exercice IV. Résoudre le système :

A l'aide des polynômes symétriques élémentaires, on cherche les coefficients d'un polynôme du troisième degré dont ces trois nombres sont les racines.

Avec les notations ci-dessus, on réécrit le système :
  • d'où
  • d'où

On écrit maintenant le polynôme P du troisième degré donné par les formules de Viète : , soit X3 - X2 - 10X +10 =0. Une racine évidente est x=1. Ensuite, soit on factorise P, soit on calcule la somme et le produit des deux autres racines pour écrire le facteur de degré deux dans P.

Pour la seconde méthode, de la première ligne du calcul des , et , on tire y+z=0 et de la deuxième y+z+y z = y z = -10. Les nombres y et z sont racines de X2-10.

Les solutions du système sont

Formule de Cardan

Résolution par radicaux d'une équation polynomiale

Ici nous montrons comment la résolution complète des équations du troisième degré, même à racines réelles, nécessite, dans certains cas, l'utilisation des nombres complexes. Ce problème est à l'origine de la définition des nombres complexes (voir Ensembles de nombres et équations ).

On sait résoudre les équations du second degré en utilisant des racines (carrées). On obtient des solutions dans ou dans . On peut se poser la question de savoir si l'on peut résoudre des équations de degré supérieur : 3, 4, 5, 6... en écrivant les solutions avec des racines (carrées, cubiques, etc.). La théorie de Galois répond que c'est possible pour les degrés 3 et 4 et impossible au-delà.

Étude du degré 3

Pour les équations de degré 3 à coefficients réels, les solutions sont données par les formules de Cardan. La forme générale d'une l'équation de degré 3 est : a x3+b x2+c x+d=0 avec réels et .

Réduction du terme en x2

Pour simplifier la tâche, on peut aisément éliminer le terme en x2 en divisant par a, puis en posant , ce qui conduit à une nouvelle équation équivalente de la forme : z3+p z+q = 0 avec ( p , q) dépendant de a,b,c,d. C'est un calcul simple à faire.

Introduction des inconnues u et v

La suite passe par une idée, due aux mathématiciens Cardan et Tartaglia, celle de chercher des solutions de la forme z=u+v (en se gardant, comme on le verra, la possibilité de préciser encore u et v), puis de se ramener à une équation du second degré.

En posant z=u+v, on peut écrire :

On fait alors le choix de poser . Ceci implique alors de résoudre le système :

Nous parlons d'implication et pas d'équivalence, ce qui impliquera quelques précautions qui seront examinées en dessous...

On pose alors U=u3 et V=v3. On a alors fait apparaître les valeurs de U+V et de U V, par conséquent U et V sont les solutions de l'équation du second degré (Et) : dont le discriminant est

Formule de Cardan dans le cas

Formule de Cardan.

Si 4p3+27q2 est strictement positif, le polynôme z3+p z+q admet au moins la racine réelle

On peut aussi l'écrire sous la forme :

Démonstration.

Dans le cas , les solutions de (Et) sont : , c'est-à-dire, par exemple, puisque u et v jouent des rôles symétriques :

et

On peut ensuite calculer u et v, en prenant leurs racines cubiques (on est ici dans , un nombre n'a qu'une seule racine cubique) et ensuite z=u+v. Réciproquement, les valeurs trouvées pour u et v vérifient et u+v est bien solution de l'équation.
Exemple. Résoudre l'équation z3-3z+9=0.

Commentaires sur la formule de Cardan

Et les autres solutions ?

La formule de Cardan établie dans ne fournit qu'une seule racine réelle (alors qu'il peut en exister trois), et ceci uniquement si 4p3+27q2 est strictement positif. Si on raisonne dans , alors les valeurs de U et V trouvées dans la démonstration de cette page ont chacune trois racines cubiques, réelles ou complexes u,j u,j2 u pour U et v,j v,j2 v pour V ce qui fait neuf choix possibles pour le couple (u,v). On a mentionné plus haut une implication qui n'est pas une équivalence et on a trouvé neuf candidats solutions dont toutes ne peuvent pas convenir.

Pour trouver les "bonnes" solutions, il suffit les tester dans l'équation... Cette vérification en élimine six, il reste trois choix pour les racines de U et de V qui fournissent des solutions à l'équation. Les voici :

La première est réelle, et les deux autres sont complexes conjuguées du fait de et .
Toutes les racines dans le cas

Lorsque 4p3+27q2 est strictement positif, on peut calculer une racine réelle du polynôme en se limitant à , et, dès lors que l'on connaÎt , ensemble inconnu par Cardan et Tartaglia, les deux autres racines qui sont conjuguées.

C'est la résolution complète par radicaux de l'équation de degré 3 dans le cas où . Notons que la formule de Cardan permet ici de trouver la racine réelle, mais que la connaissance des deux autres (complexes conjuguées) nécessite la connaissance de .
Le cas va permettre une introduction de ...

Que se passe-t-il si 4p3+27q2 est strictement négatif ?

Un calcul osé dans un exemple

L'application de la formule de Cardan par Bombelli, mathématicien du XVI-ième siècle, à l'équation z3-15z-4=0 (qui possède une racine facile à deviner : z0 = 4) conduit à . Une impasse à cette époque où les nombres complexes n'ont pas encore été introduits. À cette racine de -1 qui n'existe pas, Bombelli ose donner un nom (ce nom sera définitivement établi par Euler) : disons i, (début d'imaginaire !) avec , cette racine s'écrit (continuons d'oser!) . Il est alors assez facile de vérifier, ce que Bombelli fait avec ses règles de calcul, que :

et

autrement dit

et

On obtient alors ... et on retrouve la racine connue de l’équation ! Les calculs "osés" de Bombelli ont permis de retrouver le résultat. Historiquement, c'est ce qu'on appelle une coupure épistémologique dans la science, qui ouvre la voie à l'introduction des nombres complexes...

Traitement du cas 4p3+27q2 < 0

On suppose connue maintenant l'existence de . On reprend la démonstration de la formule de Cardan dans le cas où 4p3+27q2 est strictement négatif. Alors on écrit et le résultat de la résolution de l'équation (Et) devient :

et .

On remarque que V et U sont conjugués et on obtient à nouveau 9 couples (u,v) , avec . Là encore, trois seulement sont solutions, les autres étant éliminés après test dans l'équation :

Toutes les racines dans le cas

Lorsque 4p3+27q2 est strictement négatif, on peut calculer les trois racines réelles du polynôme en utilisant les nombres complexes.

On notera avec beaucoup d’intérêt que ces trois racines sont réelles (puisqu'égales à leurs conjuguées), mais qu'il a fallu passer par les nombres complexes pour les obtenir...

Transformation de Fourier discrète (TFD)

La transformation de Fourier discrète (TFD) est un outil mathématique de traitement du signal numérique. Elle utilise des fonctions exponentielles complexes, raison de la présence de ce chapitre ici. On en présentera ici une approche simple, limitée à des fonctions périodiques (voir ce cours sur les fonctions périodiques ).

Problème

Donnons un aspect rapide du problème. On appelle signal une quantité dépendant du temps. Une fonction, la courbe des cours de la Bourse, un enregistrement météo, un son ... Certains de ces signaux sont périodiques.

Exemple de fonction périodique : La fonction de la variable t (le temps) et de période T avec représentée par la courbe ci-dessous est définie par pour , et par périodicité ailleurs.

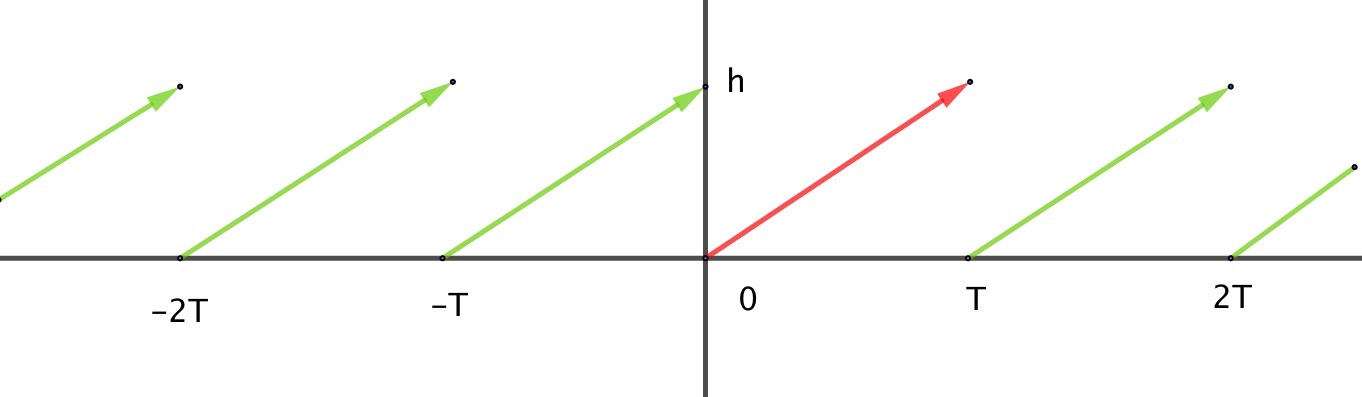
figure

A la notion de période T, on ajoute les notions (vues en physique) de fréquence f et celle de pulsation d'un phénomène périodique. Ces notions sont reliées par les relations : .

Analyse du problème

Pour comprendre les étapes, mais sans trop rentrer dans les détails, on peut donner l'exemple de l'enregistrement, puis la restitution d'une musique à l'aide d'un CD. L'enregistrement se fait avec un micro, c'est un processus analogique. L'écoute se fait avec des hauts parleurs, c'est également un processus analogique. Entre les deux, le son doit être transformé, il est analysé et numérisé. La TFD permet de relier les intensités du son aux fréquences des éléments (harmoniques) qui le constituent

Soit s un signal, périodique de période T. La fréquence fondamentale du signal est .

Si on fait tracer la courbe de s sur un écran, on obtient une courbe continue ou continue par morceaux dont l'équation est en général inconnue. Nous indiquons à cette page un théorème hors programme affirmant que, sous de bonnes hypothèses, la fonction s peut être approchée par une fonction somme de cosinus ou de sinus.

Analyse temporelle par l'échantillonnage

Afin de diminuer la complexité des calculs sur un signal, on recourt à deux simplifications indiquées ci-dessous : c'est le principe de l'échantillonnage.

  1. On se limite à un intervalle de temps borné, par exemple une période , que l'on divise en N intervalles de temps ( N entier) : .
  2. En chacun des instants ti ), on mesure les intensités prises par le signal. On obtient ainsi une suite .

Ce processus est l'analyse temporelle du signal qui a été ainsi échantillonné par la suite . Pour rendre compte de la complexité d'un signal ou de la richesse de ses harmoniques il faut que N soit très grand. Pour donner un ordre d'idée, le son reproduit par un CD est échantillonné fois par seconde.

Le dessin de gauche, ci-dessous, représente la courbe d'un signal (ici ), celui de droite montre un échantillonnage, une numérisation de la courbe. Les valeurs xi sont les ordonnées des extrémités supérieures des segments rouges.

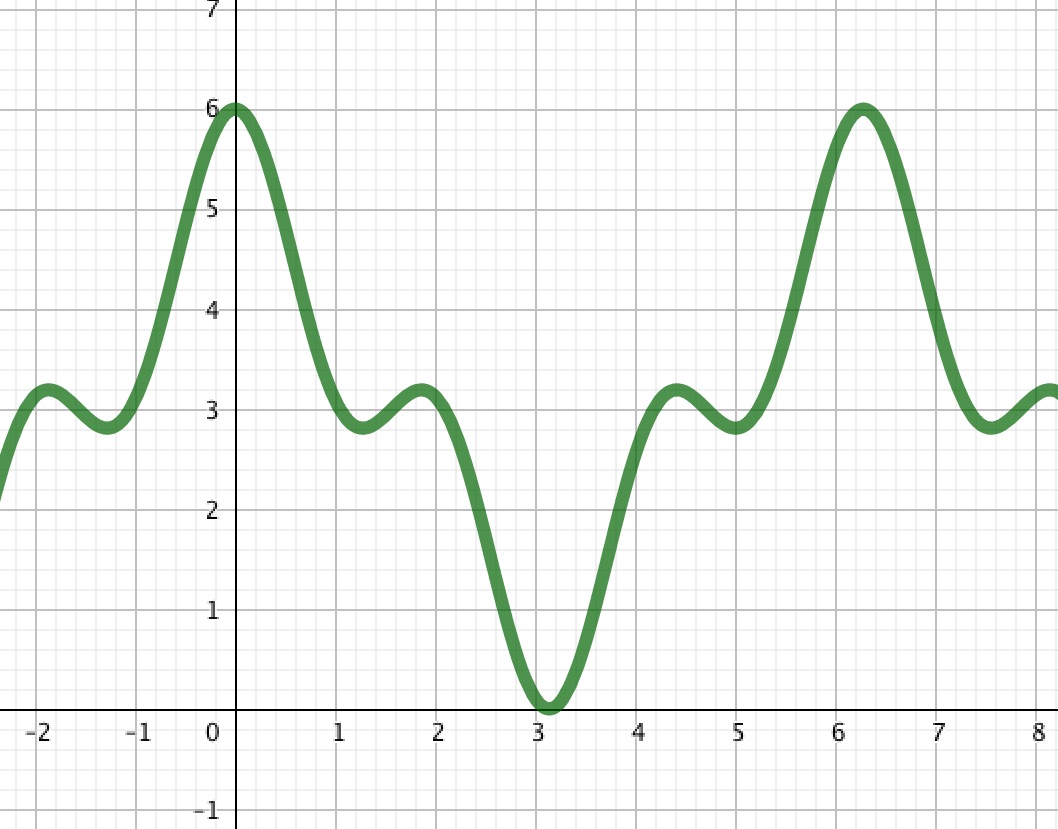
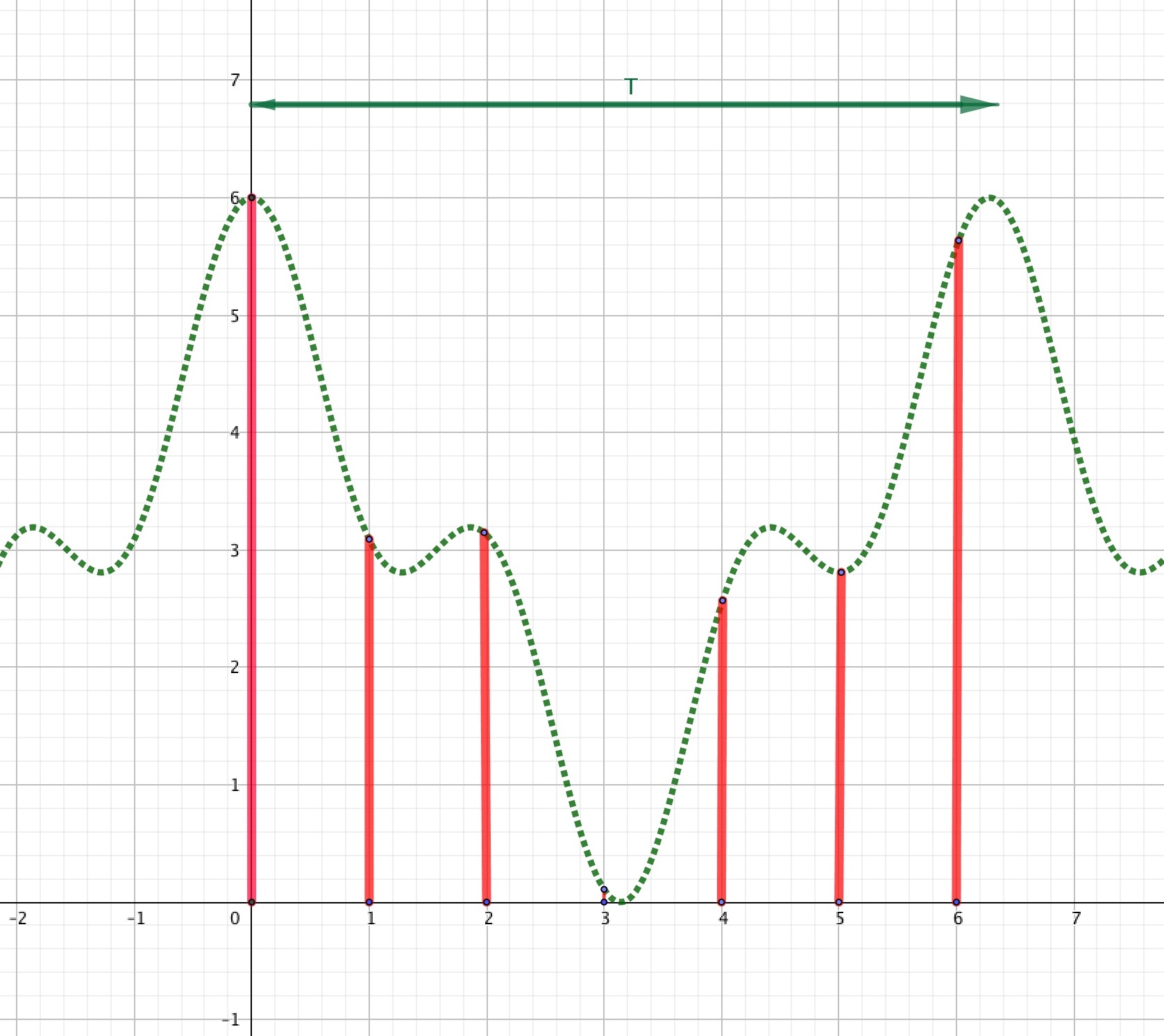
figure figure

Analyse fréquentielle

Le signal (son) est, comme on le voit dans le théorème , la somme de ses harmoniques. Ces harmoniques sont associés à des fréquences fk multiples de la fréquence fondamentale f1 et on souhaite pouvoir représenter ces fréquences ainsi que l?importance de chacune d'entre elles. Le résultat de ce travail sera une courbe du type de celle figurant au bas de cette page (courbe "en peigne"), où chaque fréquence fk est repérée en abscisse par une barre dont la hauteur correspond à son importance.

[En fait, dans la pratique, plutôt que d'utiliser des sommes de fonctions trigonométriques, il est plus commode d'utiliser des sommes de fonctions exponentielles complexes de type avec , sachant que le lien trigonométrique/exponentielle se fait par les formules d'Euler. ]

La transformation de Fourier discrète (TFD) permet d'arriver à ce résultat, en calculant, à partir de la suite , une suite où les valeurs représentent la part de la fréquence fk dans le signal.

Aux nombres complexes on associe les fréquences .
La suite ( ) constitue le spectre des fréquences qui complète l'analyse temporelle obtenu par l'échantillonnage. On verra à la page suivante une illustration de ces résultats.

Lorsque le nombre N d'échantillons est suffisamment grand, le spectre des fréquences se rapproche du spectre harmonique du signal, c'est-à-dire de l'ensemble des harmoniques inclus dans le son et qui lui donnent sa richesse. Voici ci-dessous un exemple de spectre des fréquences.

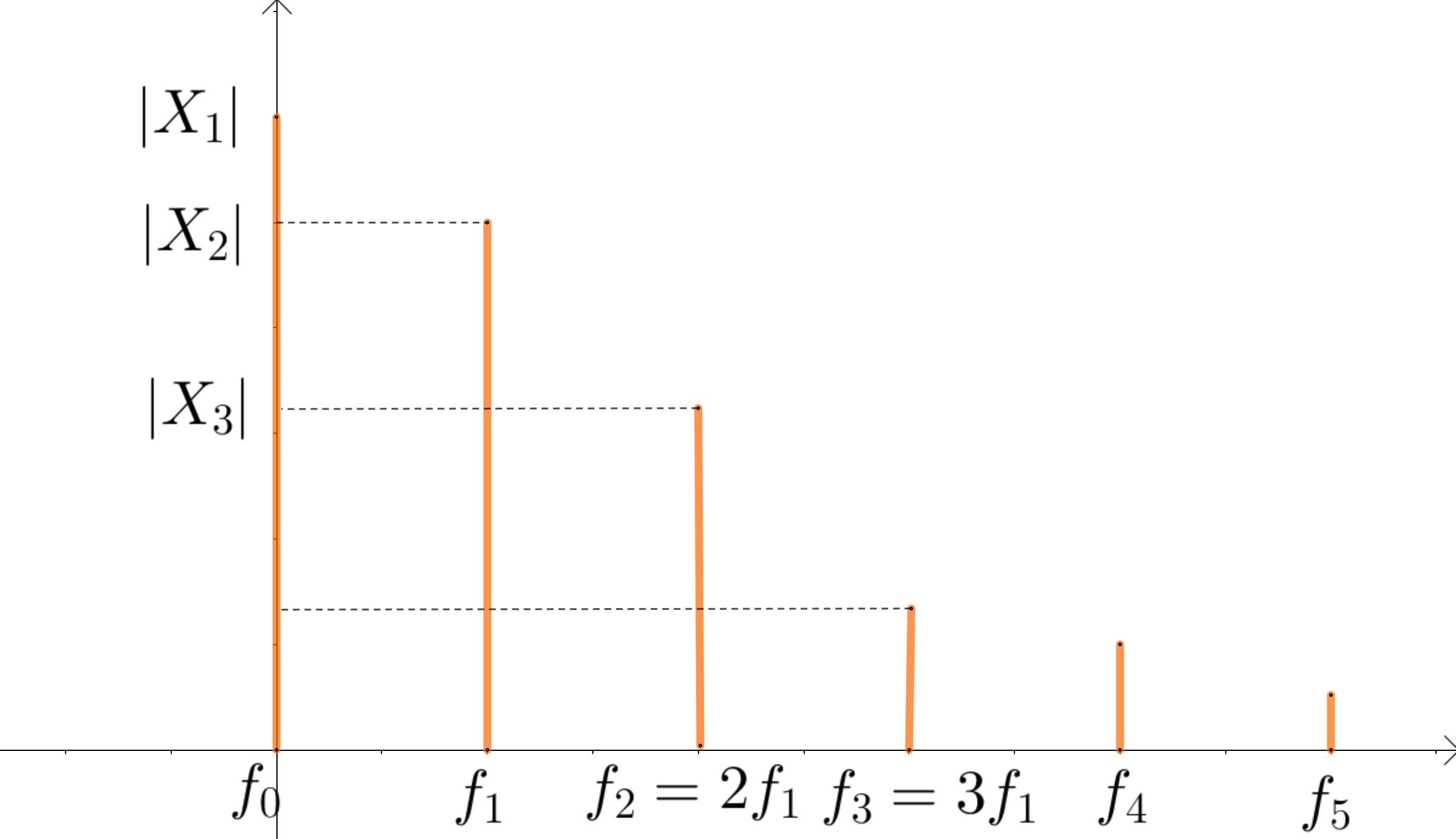
figure

Exemples et exercices sont en page suivante TFD : Définition, exemples, exercices .

Théorème d'approximation d'un signal

L’éventuelle complexité de ce qui suit autorise à n'en lire que les cinq dernières lignes : le résultat principal. On admet donc le théorème suivant :

Théorème.

Soit K un entier. Toute fonction, tout signal périodique, suffisamment régulière, où t est le temps, peut être approchée (et ceci d'autant mieux que K est grand) par une fonction somme de cosinus sous la forme :

.

Cette video La formule de Joseph Fourier. Du sinus de l'antiquité aux fichiers mp 3 de Canal U illustre bien ce théorème.


Diverses définitions.

Les nombres ck et sont des constantes, f1 la fréquence fondamentale du signal. On note .
Le terme de rang k : s'appelle l'harmonique de rang k du signal. Il est défini par son amplitude ck et son décalage de phase (qui ne nous intéresse pas ici).

Avec ces notations la fonction s'écrit :

Plus K est grand, plus , la somme des harmoniques, est proche du signal s.

TFD : Définition, exemples, exercices

Cette page propose des exemples et exercices de calcul de la TFD ainsi qu'un bref alinéa sur une application.

Définition.

Soit N un entier supérieur ou égal à 1 et une suite de N valeurs . On pose, pour :

On appelle transformation de Fourier discrète (TFD) la transformation définie par :

TFD

Exemple I.

Transformée de Fourier discrète de la série (0,1,0).

On calcule : et on obtient

Exemple II.

Calcul de la TFD d'un signal sur une fenêtre I découpée en quatre intervalles



Valeurs du signal t -> x(t)


Dénominateurs

Fonction signal E [ t --> x(t) ]

Courbe du signal t -> x(t)

Valeurs de la fonction spectrale u -> X(u)








} }
Fonction spectrale : modules T_0,T_1,T_2,T_3 de X_0,X_1,X_2,X_3



Parties réelle et imaginaire avec 2décimales


Fonction spectrale F [ u --> X(u) ]

Courbe du spectre k -> X(k)

Tableau des 2 courbes
et N = 4
4 intervalles de 0 à 4

4 échantillons
t0=0, 2,1,2,3,20 = 2,
t1=1, 2,1,2,3,21 = 1,
t2=2, 2,1,2,3,22 = 2,
t3=3, 2,1,2,3,23 = 3
Courbe du signal : Spectre :

Remarques.

  1. L'échantillonnage est visualisé sur la courbe de gauche par les pointillés rouges. Le spectre des fréquences est représenté à droite par les barres verticales bleues. La courbe spectrale représentée en pointillé bleu n'a pour cet exercice que peu de sens, elle ne devient significative que si le nombre N d'échantillons est suffisamment grand.
  2. Pour simplifier, les graduations de l'axe des abscisses de chacune des figures ci-dessus ont été ramenées par des changements d'échelles aux valeurs 0,1,2,3 qui sont de simples numéros.
  3. En réalité, on échantillonne la fonction avec en abscisse les N valeurs suivantes : .
Solution. On calcule :
  • X0 = 2+1+2+3 = 8
D'où le résultat , et pour les modules .
dessin

Applications de la TFD au traitement du signal

Dans un système électronique (S), un signal-entrée : à l'entrée d'une boîte noire en ressort sous la forme d'un signal-réponse . Il est souvent instructif de comparer les spectres de fréquences entrée et sortie en faisant varier la forme et les paramètres du signal-entrée, pour obtenir un résultat souhaité.

En Électronique notamment, la TFD permet d'adapter les caractéristiques du système (S) dans le but d'obtenir un spectre du signal-réponse de type donné.
Exercices.
  1. Transformée de Fourier discrète de la série
    Solution.

  2. Transformée de Fourier discrète de la série (1,1,1)
    Solution.

    TFD(1,1,1)=(3,0,0)

  3. Transformée de Fourier discrète de la série avec N termes égaux à 1.
    Solution.

Ensemble de Mandelbrot, quelques résultats.

Définition. Soit c un nombre complexe. On définit une suite complexe par la relation de récurrence :

On appelle ensemble de Mandelbrot, noté M, l'ensemble des nombres complexes c pour lesquels cette suite est bornée.

Cet ensemble M est la célèbre fractale de Mandelbrot représentée en noir dans la figure ci-dessus. La propriété d'un objet fractal est d'avoir la même structure à toute échelle. Consulter cette page Wikipedia.

Quelques résultats à démontrer.

Pour ces démonstrations, l'inégalité triangulaire sous sa forme complète sera utile, et on l’utilisera parfois avec des inégalités dans l'autre sens :

Si 2,1,2,3,2 et y sont deux nombres complexes quelconques, alors on a la double inégalité suivante :

Exercice.
  1. Montrer pour tout n dans l'égalité : . En déduire que l'ensemble des images dans le plan complexe des nombres c tels que c appartienne à M est symétrique par rapport à l’axe des abscisses. Dorénavant, on notera zn(c) = zn.
    Solution. On procède par récurrence. L'hypothèse de récurrence, à un rang n, est : . L'initialisation est immédiate, est vraie. Pour l'hérédité, montrons que est vraie : De , on peut écrire, grâce à l'hypothèse de récurrence et aux propriétés du module et du conjugué,

    .

    Donc est vraie, ainsi que , d'où le résultat..

    Par ailleurs, si la suite est bornée, alors l'est aussi, ainsi que . On en déduit que si , alors . En d'autres termes l'ensemble des images dans le plan complexe des nombres c tels que c appartienne à M est symétrique par rapport à l'axe des abscisses.

  2. Calculer z1, z2 et z3. Montrer que zn s'écrit comme un polynôme en c. Quel est son degré ?
    Solution. On calcule
    • z1 = c, z2= c2+c, z3= c4+2c3+c2+c.
    • Par récurrence. z1 est un polynôme. Supposons que zn le soit. Alors . Le carré d'un polynôme est aussi un polynôme. Donc également. D'où le résultat.
    • Sur les premières valeurs, il semble que l'on puisse faire l'hypothèse que, pour le degré de zn est (hypothèse de récurrence). C'est vrai pour n=1 et n=2. Supposons le résultat vrai au rang n. Le degré de est le double de celui de zn, il est égal à . D'où le résultat.
  3. Soit p un entier naturel et une suite non constante. On dit qu'elle est stationnaire à partir de zp si les deux conditions suivantes sont vérifiées :
    • pour tout l'égalité zp = zn est vérifiée.
    • Si , zp est différent de .
    • Montrer que si, pour un entier naturel q, on a , alors tous les termes d'indice supérieur à q ( zq et les suivants) sont tous égaux à zq.
      Solution. On considère la propriété : Pour tout . Elle est initialisée au rang q. Alors de , on tire et, par définition de la suite, . C'est ce que l'on voulait démontrer. En résumé, est vraie et pour tout . En conclusion, la suite est stationnaire à partir de zq.
    • Donner une condition nécessaire et suffisante pour que tous les termes de la suite soient nuls. La suite peut-elle être stationnaire à partir de z1 ?
      Solution.

      Si les termes de la suite sont nuls alors c=0. Réciproquement, si c est nul, tous termes de la suite sont nuls.

      Conclusion : la suite est la suite nulle si et seulement si c est nul.

      Si la suite est stationnaire à partir de z1, alors z0=0, z1=c, z2 = c2+c = z1=c. Donc c est nul, et la suite est la suite nulle. Elle ne peut donc pas être stationnaire à partir de z1.

    • Montrer que si deux termes consécutifs de la suite sont nuls alors tous les termes de la suite sont nuls.
      Solution. Soit un entier naturel q tel que . Alors de , on tire c= 0. Or, si c est nul, d'après la question précédente, la suite est la suite nulle.
    • On suppose maintenant que c est non nul et p supérieur ou égal à 2. Montrer que la suite est stationnaire à partir de zp si et seulement si .
      Solution.

      Supposons d'abord : . Alors on a :

      .

      On conclut à l'égalité de tous les termes à partir de p comme en (i) et comme et -zp sont opposés et non nuls ensemble (voir (iii)), la deuxième condition de la définition est vérifiée.

      Réciproquement, supposons maintenant la suite stationnaire à partir de zp. On a les implications suivantes grâce à la définition de la suite :

      .

      Puisque la suite est stationnaire à partir du rang p+1, la condition (b) s'écrit et on obtient l'égalité

    • La suite peut-elle être stationnaire à partir de z2? Quelle est cette suite ?
      Solution.

      Par définition, z0 = 0, z1 = c, z2 = c2+c. On utilise la caractérisation de la question précédente : z1+z2=0, dont on tire z2= -c et donc c2+c= -c, soit c2+2c=0.

      L'équation c2+2c=0 a deux solutions : c=0 (pour cette valeur, on a vu que la suite est nulle) et c= -2. Pour c= -2, les termes sont (). La suite est stationnaire à partir de z3 et prend ensuite la valeur 2.

  4. On suppose dans cette question que p est la plus petite valeur de n telle que la suite soit 2-périodique (et non stationnaire) à partir de zp, c'est-à-dire vérifie . Le suite peut-elle être 2-périodique à partir de z0 ? Donner ses valeurs. Mêmes questions à partir de z2.
    Solution.
    • Si la suite est 2-périodique à partir de z0, alors, z0=0, z1=c, z2=c2+c=0... Deux valeurs conviennent c=0 (exclus, la suite est nulle) et c= -1. Dans ce dernier cas, la suite est bien 2-périodique (Vérifiez-le). Les termes sont : .
    • Si la suite est 2-périodique à partir de z2. Alors on reprend les résultats de la question 2 et on calcule z4 = z32+c = (c4+2c3+c2+c)2 +c ; par périodicité, on obtient l'équation : (c4+2c3+c2+c)2 +c =c2+c La résolution de cette équation (à la main (faisable) ou avec un logiciel de calcul !) fournit (en dehors de 0) 4 solutions : {}
      • Dans le cas c = -2, on a vu à la question précédente que la suite est stationnaire à partir de z2. On rejette donc cette valeur.
      • Dans le cas c= -1, on a vu au début de cette question que la suite est 2-périodique, mais à partir de z0. On rejette donc cette valeur.
      • Dans le cas , cette valeur convient et les termes de la suite sont :
      • Dans le cas , cette valeur convient et les termes de la suite sont :
  5. On va montrer que M est inclus dans un cercle de centre O. On suppose . Prouver que pour tout , on a les résultats suivants :
    • Solution. Par récurence. Pour . Hérédité : on suppose qu'à un rang n on a : , et on va utiliser la partie de l'inégalité triangulaire :

      et la définition de la suite pour écrire cet enchaînement d'inégalités :

      On en déduit donc l'inégalité .
    • Solution. On peut écrire pour :
    • .
      Solution. Preuve à nouveau par récurrence. Il est facile de voir que la propriété est vraie pour n=1, puisqu'on a . Supposons la propriété vraie au rang n. Alors, au rang n+1, on utilise le résultat précédent (voir (iii)) :

      Ce qui achève la preuve.
    • Montrer maintenant que M est inclus dans un cercle de centre O.
      Solution. Dans le cas , on a : donc, d'après la question précédente, on en déduit () et la suite n'est pas bornée ; donc c n'appartient pas à M.
      Conclusion : est ainsi une condition nécessaire pour que la suite (zn) soit bornée. L'ensemble M est donc inclus dans le cercle de centre O d'affixe 0 et de rayon 2.

cours sur les nombres complexes du point de vue algébrique.
: racine de l'unité,roots,squareroot,factorization,equations,nombre complexe, polynomials,fourier_transform,formules de Viète, Formule de Cardan, ensemble de Mandelbrot, interactive mathematics, interactive math, server side interactivity

The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.