Changement de variables
Objectifs
La méthode du changement de variable est très utile pour le calcul d'intégrale ou de primitive ; elle peut conduire à des erreurs si elle n'est pas appliquée avec soin. On peut aussi se compliquer la vie inutilement si on l'applique de travers.Guide
Le théorème
Théorème :
Soit
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
Cas où le changement de variables est évident
On doit calculer ; on voit que x apparaît toujours par l'intermédiaire d'une expression plus complexe et de sa dérivée :
,
on fait alors le changement de variable
:
On applique à la fonction
f le
théorème.
Soit
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
Concrètement, on vérifie que la fonction
 est
C1 sur
et on remplace
est
C1 sur
et on remplace
On obtient ainsi une nouvelle intégrale
égale à l'intégrale
.
 est
C1 sur
et on remplace
est
C1 sur
et on remplace
| par | u | |
| par | du | |
| les bornes a et b | par | et . |
Remarque : Quand x vaut a, la nouvelle variable vaut ...
Exemple
Exemple
Pour voir le théorème en même temps.
Soit
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
Calculons dx. La fonction à intégrer est de la forme f(x4) où est la dérivée de et où f est la fonction définie par f(u)= u5. On fait donc le changement de variable u=x4 :
- On prend f(u)=u5 et .
-
On vérifie que
 est une fonction
C1 sur l'intervalle [4,6].
est une fonction
C1 sur l'intervalle [4,6].
- On vérifie que f est une fonction continue sur l'intervalle .
- Puis on remplace
x4 par u dt par du les bornes 4 et 6 par 44 et 64
On obtient donc :
.
Cas où le changement de variables n'est pas évident
On peut aussi utiliser la formule du théorèmeSoit
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
de la droite vers la gauche. Pour calculer
où
f est une fonction continue sur
, on a envie de poser
.
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
Contrairement à ce qu'il est souvent écrit, on n'a pas besoin de définir la fonction réciproque de
 . Par contre, il est essentiel de trouver un intervalle
tel que
. Par contre, il est essentiel de trouver un intervalle
tel que
- la fonction
 est définie, de classe
C1 sur
et vérifie
et
est définie, de classe
C1 sur
et vérifie
et
- la fonction f est continue sur (attention, peut être plus grand que ).
Soit
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
pour faire le changement de variable
:
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
.
Concrètement, une fois choisie la fonction
 :
:
Remarque :  :
:
- on choisit a et b vérifiant et et on détermine l'intervalle ;
-
on vérifie que
 est
C1 sur l'intervalle
;
est
C1 sur l'intervalle
;
- on vérifie que f est une fonction continue sur ; c'est immédiat dans le cas ;
- on remplace
x par dx par les bornes  et
et
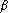
par a et b
-
En général, on choisit
a et
b de manière à ce que la fonction
 soit bijective de
sur
, et en particulier
tel que
soit égal à
:
par exemple dans le cas où le changement de variables est
x=cos(u) avec les bornes
soit bijective de
sur
, et en particulier
tel que
soit égal à
:
par exemple dans le cas où le changement de variables est
x=cos(u) avec les bornes
 =0 et
, personne n'aurait l'idée saugrenue de prendre
et
b=80
=0 et
, personne n'aurait l'idée saugrenue de prendre
et
b=80 si la fonction
f est définie sur
. Mais c'est permis !
si la fonction
f est définie sur
. Mais c'est permis !
-
En aucun cas, il n'est nécessaire que la réciproque de
 soit
C1.
soit
C1.
Exemple typique
Pour voir le théorème.Soit
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
 une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
C1 définie sur l'intervalle
.
Soit
f une fonction continue sur l'intervalle
. On a l'égalité :
On veut calculer l'intégrale
.
On a envie de poser
x=cos( t) et de prendre comme fonction
 la fonction définie par
sur un intervalle à déterminer.
la fonction définie par
sur un intervalle à déterminer.
- La fonction
 est
C1 sur
. On choisit deux nombres
a et
b
tel que cos(a)= -1 et cos(b)=1,a=
est
C1 sur
. On choisit deux nombres
a et
b
tel que cos(a)= -1 et cos(b)=1,a= et
b=0
par exemple.,
On peut aussi prendre a= -7
et
b=0
par exemple.,
On peut aussi prendre a= -7 et
b=6
et
b=6 ;
mais bien sûr, jamais personne ne fera cela !
;
mais bien sûr, jamais personne ne fera cela !
L'image de est de toute façon contenue dans [-1,1] (et même égale).
est de toute façon contenue dans [-1,1] (et même égale).
- La fonction f définie sur [-1,1] par est continue sur [-1,1] ;
-
On obtient par le théorème :
 .
Il ne reste plus qu'à finir les
calculs.
.
Il ne reste plus qu'à finir les
calculs.
Sur l'intervalle [0, ], la fonction sin est positive, on a donc :
], la fonction sin est positive, on a donc :
 et
b=6
et
b=6 ,
la fonction
sinn'aurait pas été positive entre
-7
,
la fonction
sinn'aurait pas été positive entre
-7 et
6
et
6 et le calcul aurait été moins simple !
et le calcul aurait été moins simple !
Exercices corrigés
Exercice : Vous voulez calculer
l'intégrale
.
Le théorème justifie-t-il le changement de variables
x=cos(t) pour
t compris entre
4 et
? Que vaut l'intégrale transformée ?
et
? Que vaut l'intégrale transformée ?
Solution
 et
? Que vaut l'intégrale transformée ?
et
? Que vaut l'intégrale transformée ?
Solution
Oui, le théorème s'applique :
Bien que correct, le choix de cet intervalle est tout à fait déconseillé car la suite des calculs serait très compliquée puisqu'il faudrait séparer en intervalles où sin est de signe constant pour calculer .
- la fonction définie sur l'intervalle
[
]
par
 (t)=cos(t) est
C1.
(t)=cos(t) est
C1.
-
Son image est contenue dans l'intervalle [-1,1]. On a
, cos(4
 )=1
)=1 - La fonction f définie sur [-1,1] par est continue sur [-1,1].
Bien que correct, le choix de cet intervalle est tout à fait déconseillé car la suite des calculs serait très compliquée puisqu'il faudrait séparer en intervalles où sin est de signe constant pour calculer .
Exercice :
Soit
.
Le théorème justifie-t-il le changement de variables
x=Arctan(2t) ?
Que choisirez-vous pour les bornes
a et
b de la nouvelle intégrale ?
Solution
Solution
Non, je ne peux pas trouver de nombres
a et
b vérifiant les deux conditions suivantes
Par contre en transformant astucieusement, on peut utiliser dans ce cas le changement de variable dit évident ou conseillé, c'est-à-dire transformer 1/(2+cos(x)) par les formules de trigonométrie jusqu'à tomber sur une expression de la forme . Sur quel intervalle peut-on alors prendre comme fonction la fonction donnée par
?
la fonction donnée par
?
-
Arctan(a)=0, Arctan(b)=

- la fonction est définie et C1 sur l'intervalle (ou ).
Par contre en transformant astucieusement, on peut utiliser dans ce cas le changement de variable dit évident ou conseillé, c'est-à-dire transformer 1/(2+cos(x)) par les formules de trigonométrie jusqu'à tomber sur une expression de la forme . Sur quel intervalle peut-on alors prendre comme fonction
 la fonction donnée par
?
la fonction donnée par
?
Changement de variables dans une primitive
Pour le calcul de la primitive sur l'intervalle (avec ), on applique le changement de variable si on peut-
choisir un
y vérifiant
et un
 tel que
tel que
-
vérifier que
 est
C1 sur
(ou
)
est
C1 sur
(ou
)
- vérifier que f est une fonction continue sur .
 bijectif sur
afin de pouvoir considérer la fonction réciproque
bijectif sur
afin de pouvoir considérer la fonction réciproque
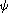 de
de
 sur
.
sur
.
Concrètement,
La primitive
F est alors définie sur
et on a en tout point
x de
- pour tout x de
, on pose y=
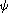 (x)
(x)
-
on vérifie que
 est
C1 sur
est
C1 sur
- on vérifie que f est continue sur .
Exemple :
Le changement de variable
u=cos(t) appliqué à
t compris entre
et Arccos(x) donne (par définition de Arccos,
sin(t) est toujours positif ou nul pour
t compris entre
et Arccos(x)) :
Exercices interactifs
Exercice :
Dérivation d'une intégrale fonction des bornes
Exercice :
Intégration interactive : changement de variables