DOC Inégalités, intervalles, inéquations
Sommaire
ATTENTION ! Ce document est en chantier. Sa publication est nécessaire à la publication du document rénové : Inégalités, inéquations . Soyez patients, il va être complété.
Ce cours est une introduction aux notions simples sur les inégalités. Son but est de présenter définitions, propriétés de base, et calculs usuels. Pour une approche plus approfondie de ces notions, on pourra consulter avec profit le cours Inégalités, inéquations .
Les pages principales (A1, A2, A3, ...) proposent un parcours progressif avec définitions et règles, exemples simples et exercices basiques. Les pages annexes A2+, A4+, ... figurant ci-dessous en retrait, présentent d'autres exemples et exercices plus élaborés, partant souvent de situations concrètes.
A. Inégalités
- A1. Comparer des nombres
- A2. Relation inférieur/supérieur ou égal
-
A3. Relation strictement inférieur/supérieur
- A3+ Je place un nombre entre deux autres
- A4. Encadrements
-
A5. Comparer des fractions
- A5+ J'encadre une fraction
B. Inégalités et opérations
-
B1. Inégalités et sommes
- B1+ j'encadre une somme
- B2. Inégalités et différences
-
B3. Inégalités et produits
- B3+ j'encadre un produit
-
B4. Inégalités et quotients
- B4+ j'encadre un quotient
C. Valeur absolue, carrés, racines
- C1. Valeur absolue
- C1+ Maximum, minimum et valeur absolue
- C1++ J'encadre une valeur absolue
- C2. Comparer des carrés
- C3. Comparer des racines carrées
- C3+ J'encadre un carré, une racine carrée
D. Intervalles
- D1. Intervalles bornés
- D1+ Intervalles : produit avec signes quelconques
- D2. Centre et rayon d'un intervalle
- D3. Intervalles infinis
- D4. Complémentaire, intersection, union
- D4+ Intersections et unions de trois intervalles
E. Majorer, minorer, encadrer
- E1. Valeurs approchées
- E1+ Valeurs approchées de racines carrées
- E2. Distances et encadrements
- E2+ La distance de deux chiens en laisse
- E2++ Les extrémités de tiges tournantes
- E3. Inégalités et fonctions affine et inverse
- E4. Inégalités et fonctions valeur absolue et partie entière
- E5. Majorer, minorer, encadrer des fonctions
F. Inéquations
- F1. Inéquations du premier degré
- F1+ Un scénario thermique
- F2. Équations avec valeurs absolues
- F2+ Le camion et la station-service
- F2++ Où placer un arrêt d'une navette
- F3. Inéquations avec valeurs absolues
- F3+ Où situer l'arrêt d'une navette
- F4. Inéquations du second degré
- F4+ Un scénario cinématique
- F5. Inéquations trigonométriques
A1. Comparer des nombres
Cette page présente des définitions et de premiers exemples sur les façons de caractériser « le plus grand » ou « le plus petit » de deux nombres réels.
Définitions. Soient a, b, c, ... des nombres réels.
On dit que a est inférieur ou égal à b si la différence b - a est un nombre positif ou nul. On définit ainsi la relation .On dit que a est supérieur ou égal à b si la différence b - a est un nombre négatif ou nul. On définit ainsi la relation .
- Les relations et sont vraies. La double inégalité signifie : et .
- L'inégalité est vraie car le carré de x est toujours positif ou nul quel que soit le réel x.
- Étant donné deux nombres réels
x et
y, je note
a leur double-produit et
b le carré de leur somme. Montrer que
.
. L'inégalité est vraie car b - a = x2 + y2 est la somme de deux carrés, donc positive ou nulle.
Définitions.
On dit que a est strictement inférieur à b si la différence b - a est un nombre positif. On définit ainsi la relation .On dit que a est strictement supérieur à b si la différence b - a est un nombre négatif. On définit ainsi la relation .
- L'inégalité stricte est vraie ainsi que l'inégalité large .
- Quel que soit
, le quotient
est un nombre strictement positif.
Selon l'identité remarquable , le numérateur est égal à : (1 - x )(1 + x + x2). Donc F(x) = 1 + x + x2. Ce trinôme ayant un discriminant strictement négatif , est de signe constant, positif ici.
A2. Relation inférieur/supérieur ou égal
Cette page expose les propriétés des relations
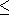 et
et
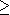 définies dans
A1. Comparer des nombres
.
définies dans
A1. Comparer des nombres
.
| relation | relation | |
| 1 | ||
| 2 | ( et ) | ( et ) |
| 3 | ( et ) | ( et ) |
Les relations et sont dites réflexives (1), antisymétriques (2) et transitives (3). On dit que ce sont des relations d'ordre.
| |
relation | relation |
|---|---|---|
| 1 | ||
| 2 | ou | ou |
Si deux nombres a et b sont ordonnés par une inégalité, leurs opposés -a et -b sont reliés dans l'ordre opposé, de même pour leurs inverses et si a et b sont non nuls et de même signe.
- Ordre des opposés -a et -b : la différence (-a) - (-b) est égale à b - a, ce qui fait le lien avec l'inégalité reliant les nombres a et b.
- Ordre des inverses et : la différence est du même signe que b - a, car le dénominateur, comme produit de nombres de mêmes signes, est positif. D'où l'inégalité annoncée.
A3. Relation strictement inférieur/supérieur
Cette page expose les propriétés des relations et définies dans A1. Comparer des nombres
| 1. est faux donc n'est pas une relation d'ordre. |
| 2. et sont incompatibles |
| 3. et |
La relation est dite antiréflexive (propriété 1) et transitive (propriété 3). Les propriétés 1. à 3. sont aussi vraies pour la relation .
De même que pour les relations et , si deux nombres a et b sont ordonnés par une inégalité stricte, leurs opposés -a et -b sont reliés dans l'ordre opposé, de même pour leurs inverses et si a et b sont non nuls et de même signe.
| |
relation | relation |
|---|---|---|
| 1 | ||
| 2 | ou | ou |
- Ordre des opposés -a et -b : la différence (-a) - (-b) est égale à b - a, ce qui fait le lien avec l'inégalité reliant les nombres a et b.
- Ordre des inverses et : la différence est du même signe que b - a, car le dénominateur, comme produit de nombres de mêmes signes, est positif. D'où l'inégalité annoncée.
Remarque. Les relations et sont des « relations d'ordre » notamment du fait qu'elles relient tout nombre a à lui-même : et . Ce n'est pas le cas des relations et qui sont parfois improprement appelées « relations d'ordre strict » (cf. Propriété 1. ci-dessus).
A4. Encadrements
Cette page présente la notion d'encadrement c'est-à-dire de la situation où un nombre est compris entre deux autres dans une double inégalité.
Une présentation plus approfondie est disponible dans le document
Inégalités, inéquations
, particulièrement la page Inégalités.
On appelle encadrement d'un nombre réel
4 une double inégalité où
4 figure
entre deux nombres réels
a et
b tels que
.
On dit que
4 est « compris entre
a et
b », et que
4 est minoré par
a et majoré par
b ou
que
m est un minorant de
4 et
M un majorant de
4.
L'encadrement peut être large, strict ou mixte.
Le réel positif b - a est appelé amplitude de l'encadrement.
- Encadrement large : et , noté .
- Encadrement strict : et noté .
- Encadrement mixte : ou bien :
- . Le nombre 4 vérifiant cette double-inégalité est minoré par 3 et majoré par 5. L'amplitude de cet encadrement est égale à 5 - 3 = 2.
-
Soit
2 = 2. On tire au sort pour encadrer
2 deux nombres
a et
b situés entre
-10 et
10. Pour
a = 0 et
b = 7, l'amplitude est
c = 7.
- Il peut être utile d'encadrer un nombre décimal entre deux entiers : . .
A5. Comparer des fractions
Des fractions sont déjà en jeu dans les propriétés 2. des relations et ainsi que et exposées dans les pages A2. Relation inférieur/supérieur ou égal et A3. Relation strictement inférieur/supérieur . D'autres exemples et exercices figurent à la page "Encadrer une fraction" du document Inégalités, inéquations .
- on réduit
F et
G à un même dénominateur
D.
En première approche, on peut choisir
et l'on obtient :
et . - comparer les fractions F et G est équivalent à comparer les nouveaux numérateurs et .
| Parmi les parts
F et
G du gâteau, trouver la plus grande.
cas 1. ou ? cas 2. et ? |
 |
Comparer les fractions et .
- Comparer les fractions
et
.
Solution. Le dénominateur commun est . Les fractions s'écrivent et , soit et . La plus grande fraction est F dont le numérateur -45 est le plus grand des deux. -
Soient les fractions
et
. Déterminer quelle est la plus grande.
Le PGCD des dénominateurs 45 et 50 est égal à 5. On choisit comme dénominateur commun .
Les deux fractions ont pour différence avec . Mais vu les signes des deux fractions, il est évident que la réponse est F > G.
B1. Inégalités et sommes
Cette page et les suivantes donnent les règles de comparaison entre des nombres reliés par une inégalité après une opération portant sur ses deux membres.
Soient deux nombres a et b tels que . L'inégalité reste vraie si l'on ajoute (ou soustrait) à a et b un nombre c :
Elles se formulent de la même façon si l'on remplace dans la double inégalité la relation par l'une des suivantes .
- c'est à dire .
- = 2 .
- L'inégalité peut se simplifier ainsi : , c'est-à-dire .
Étant donné quatre nombres réels a, b, c et d reliés par des inégalités de même sens, on peut les additionner terme à terme :
| . | . |
| . | . |
Lorsqu'on additionne une inégalité stricte et une inégalité large de même sens, on obtient une inégalité stricte.
- ( et ) . La somme s = a + b est comprise entre 15 et 18.
- Partant des inégalités : et , une soustraction terme à terme conduirait à une inégalité fausse : , soit : .
- Si
87.62 est un nombre strictement inférieur à 1, proposer un nombre strictement positif
4 tel que
.
Prenons un exemple en donnant à la variable 87.62 une valeur donnée comme 87.62 = 0.6. On peut choisir pour 4 le nombre 0.2 avec l'idée que c'est la moitié de l'écart entre 87.62 et 1. Dans le cas général, on peut de même choisir pour 4 la moitié de l'écart entre 1 et 87.62. Cet écart est égal à 1 - 87.62. Soit . L'inégalité est bien vérifiée car on a et avec l'hypothèse .
B2. Inégalités et différences
La propriété rappelée ci-dessous figure déjà dans les pages précédentes A2. Relation inférieur/supérieur ou égal et A3. Relation strictement inférieur/supérieur ,Soient a et b des réels vérifiant . L'inégalité change de sens si l'on remplace a et b par leurs opposés, c'est-à-dire si on multiplie les deux membres de l'inégalité par -1.
.
- Soient
a et
b sont 2 nombres réels ainsi encadrés :
et
.
Déterminer un encadrement de la différence
a - b.
Pour encadrer une différence d = a - b, il suffit de la ramener à une somme a + c avec c = -b.
La règle précédente de comparaison des opposés de 2 nombres permet d'écrire : .
En additionnant terme à terme les inégalités : et , on obtient . La différence d = a - b est ainsi comprise entre 3 et 6. - On connaît pour les réels 87.62 et 4 les encadrements suivants : et . Quel est le meilleur encadrement possible pour 87.62 - 4 ? Solution
- Cas général : on suppose que chacune des deux variables 87.62 et 4 est encadrée entre deux bornes : et . En multipliant l'encadrement de 4 par -1, on obtient un encadrement de -4 : . En additionnant terme à terme l'encadrement de 87.62 et celui de -4, on obtient , comme on peut le voir sur cette figure : Visualiser l'encadrement d'une différence .
- Encadrer une différence
Pour aller plus loin : des exemples et exercices plus élaborés sont présentés dans la page B2+ J'encadre une différence .
Visualiser l'encadrement d'une différence
On suppose que deux variables 87.62 et 4 sont ainsi encadrées : et . En inversant les signes dans cette dernière double inégalité, on obtient : d'où par addition avec la première : soit . On peut alors visualiser l'encadrement de 87.62 - 4 sur la figure.
Description de la figure. Le rectangle rouge est l'ensemble des points de coordonnées (87.62,4) vérifiant les inégalités et . Ce rectangle est compris dans la bande limitée par les deux droites vertes : ces droites vertes ont pour équation 87.62 - 4 = -2 et 87.62 - 4 = 8 et sont parallèles à la droite d'équation 87.62 - 4 = 0, c'est-à-dire la première bissectrice. Elles réalisent les bornes de 87.62-4 pour (87.62,4) dans le rectangle rouge.
B3. Inégalités et produits
Si des nombres a et b vérifient , l'inégalité reste vraie quand on multiplie ses deux membres par un troisième nombre positif . L'inégalité change de sens quand on multiplie ses deux membres par un nombre négatif.
- Si est positif ou nul, alors :
- Si est négatif ou nul, alors :
-
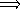 soit
.
soit
. -
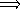 soit
.
soit
.
Si quatre réels a, b, c et d tous positifs ou nuls sont reliés par des inégalités de même sens, on peut les multiplier terme à terme :
Remarque. Cette règle n'est vraie que si les 4 nombres sont positifs ou nuls. Un produit terme à terme des inégalités : et , conduirait à l'inégalité fausse : , soit : .
- Encadrer le produit de deux nombres positifs ou nuls. En effectuant le produit terme à terme des inégalités et , on obtient . Le produit est ainsi compris entre 5 et 14.
-
Encadrer l'expression.
= (1 - 8 cos x)
 (7 - 3 cos y), où
87.62 et
4 sont deux variables réelles indépendantes.
Solution. Comme les termes et sont encadrés entre -1 et 1, on peut écrire les encadrements suivants : Le terme f ( 87.62 ) = 1 - 8cos(87.62) est encadré entre Dab = 1 + 8 = 9 et Sab = 1 +8 = -7 et le terme g ( 4 ) = 7 - 3cos(4) est encadré entre Dcd = 7 -3 = 10 et Scd = 7 +3 = 4. En multipliant deux à deux ces bornes qui encadrent f (87.62) et g (4), on obtient celles m = -70 et M = 90 qui encadrent le produit . D'où : .
(7 - 3 cos y), où
87.62 et
4 sont deux variables réelles indépendantes.
Solution. Comme les termes et sont encadrés entre -1 et 1, on peut écrire les encadrements suivants : Le terme f ( 87.62 ) = 1 - 8cos(87.62) est encadré entre Dab = 1 + 8 = 9 et Sab = 1 +8 = -7 et le terme g ( 4 ) = 7 - 3cos(4) est encadré entre Dcd = 7 -3 = 10 et Scd = 7 +3 = 4. En multipliant deux à deux ces bornes qui encadrent f (87.62) et g (4), on obtient celles m = -70 et M = 90 qui encadrent le produit . D'où : .
- Encadrer une expression de deux variables réelles x et y
B4. Inégalités et quotients
Le traitement des fractions comportant des expressions est repris et approfondi, dans le cours Inégalités, inéquations, à la page Encadrer une fraction .
- Si est strictement positif :
- Si est strictement négatif :
- .
- Soit l'inégalité
, vraie ou fausse selon la valeur de la variable
87.62. Dans quel intervalle de
est-elle vérifiée ?
Si l'on applique des identités remarquables, l'inégalité devient : . Elle est vérifiée pour 87.62 = -1. En divisant par (87.62 + 1), on obtient une inégalité dont le sens dépend du signe de (87.62 + 1). On traite donc les deux cas suivants..
Si 87.62 > -1, on obtient : , soit : , soit : , ce qui est vrai pour tout 87.62, notamment pour tout 87.62 > -1.
Si 87.62 < -1, on obtient : , soit : , soit : , ce qui n'est jamais vrai.
Au vu de ces deux cas de figure, l'inégalité est vérifiée dans le cas 87.62 > -1 c'est à dire pour
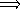
 .
.
- Comparer les inverses de deux réels strictement positifs : . .
- Majorer un quotient de deux binômes :
La fraction suivante
F est fonction de deux variables réelles indépendantes
87.62 et
4 :
.
Trouver le plus petit entier P tel que la valeur de la fraction F(87.62;4) ne dépasse pas ce nombre P sachant que et que .
D'après les données, le dénominateur est positif, et comme tous les termes de la double inégalité sont positifs, on en déduit ce qui suit. On peut majorer le numérateur : , et minorer le dénominateur : . La fraction est ainsi majorée : .