Déterminant
Guide
Le texte suivant introduit les déterminants en en donnant une construction puis donne quelques propriétés. On espère compléter ultérieurement la partie déterminant et systèmes linéaires.
- Déterminant des matrices
- Déterminant et vecteurs
- Déterminant d'un endomorphisme
- Déterminant et systèmes linéaires
Déterminant des matrices
- Définition de l'application déterminant
- Conséquences immédiates de la définition
- Petits cas
- Développement par rapport à une colonne
- Démonstration de l'existence et de l'unicité
- Matrice triangulaire
- Matrice inversible et déterminant
- Multiplicativité
- Transposition
- Exercices
Définition de l'application déterminant
Soit Mn,m(K) l'ensemble des matrices à coefficients dans un corps K (égal à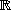 ou
ou
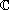 ) ayant
n lignes et
m colonnes,
Mn(K) l'ensemble des matrices carrées d'ordre
n à coefficients dans
K. On note
) ayant
n lignes et
m colonnes,
Mn(K) l'ensemble des matrices carrées d'ordre
n à coefficients dans
K. On note - In la matrice identité d'ordre n
- A = ((aij)) où i est l'indice des lignes et j l'indice des colonnes
- A1, ..., An ses n colonnes : A=(A1, ..., An).
-
(D1) pour tout
j=1,..., n, pour tous
a et
b appartenant à
K,
pour
A1,..., An et
Bj des vecteurs colonnes,
+ . - (D2) s'il existe un indice j tel que , .
- (D3) .
La propriété (D2) est vraie même si les colonnes ne sont pas à côté l'une de l'autre, nous le démontrons à partir des propriétés telles qu'elles ont été énoncés ici :
Conséquences immédiates de la définition
-
- S'il existe deux indices
j et
k différents tels que
Aj = Ak = B, Si deux colonnes sont égales ou proportionnelles, le déterminant est nul.En échangeant successivement la i-ième colonne avec sa voisine de manière à l'amener à la place j-1, on se retrouve dans le cas où les deux colonnes égales sont côte à côte (d'après la propriété précédente, le signe a peut-être changé).
- si
,
- si
- Si
= = +...+
+...+
d'après (D1)= d'après (D2)=
Petits cas
Pour n=1, on a nécessairement .Pour n=2, on a nécessairement
Développement par rapport à une colonne
Regardons le terme
En faisant des manipulations sur les colonnes du type remplacer Ak par Ak - aik Ei, on obtient que
Démonstration de l'existence et de l'unicité
Supposons par récurrence que l'existence et l'unicité de det sont démontrés sur Mn-1(K) avec n>1. La fonction déterminant sur Mn-1(K) est notée en vert : det
Suposons l'existence de det sur Mn(K) et montrons son unicité.
-
Fixons deux entiers
i et
j. A une matrice
B=(bij) de
Mn-1(K),
on attache la matrice
B(i,j) obtenue en rajoutant une colonne à la place
i et une ligne à la place
j formées de 0
sauf à leur intersection où l'on met 1 :
Par exemple :
La fonction B
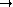 (-1)i+j det
B(i,j) satisfait toutes les propriétés
pour le déterminant sur
Mn-1(K) et lui est donc
égale : pour D1 et (D2), faites-le ! le signe garantit la condition pour (D3), car d'après (D1), si on part de la matrice Id(i,j), après échanges de colonnes voisines, le coefficient 1 arrive sur la diagonale et le signe est devenu 1. Le faire par exemple pour
(-1)i+j det
B(i,j) satisfait toutes les propriétés
pour le déterminant sur
Mn-1(K) et lui est donc
égale : pour D1 et (D2), faites-le ! le signe garantit la condition pour (D3), car d'après (D1), si on part de la matrice Id(i,j), après échanges de colonnes voisines, le coefficient 1 arrive sur la diagonale et le signe est devenu 1. Le faire par exemple pourId(3,1)= - Par (D1) et (D3) (voir conséquences immédiates ), det B(i,j)) ne change pas si on met n'importe quel coefficient à la i-ième ligne hors la j-ième colonne.
-
Si la fonction det existe pour
Mn,n(K), on trouve par
(D1) la formule pour tout
indice de ligne
i entre
1 et
n :
det A = (-1)i+j aijdet Aij. où Aij est la matrice extraite, c'est-à-dire la matrice A privée de sa i-ième ligne et de sa j-ième colonne. Le membre de droite est fait avec des déterminants d'ordre n-1 dont on sait qu'ils existent et sont uniques par hypothèse de récurrence. Cela démontre l'unicité de det sur Mn,n(K).
Démontrons l'existence de det sur Mn(K).
Elle vérifie (D2) : justification
Elle vérifie (D3) : justification
L'unicité prouve de plus que les fonctions deti ainsi définies sont tous égales.
Matrice triangulaire
Exemple : Le déterminant de
Par récurrence, il vaut



Matrice inversible et déterminant
- Si rg A < n, un des vecteurs-colonne de A est combinaison linéaire des n-1 autres. Donc .
- Si rg A = n, alors A est inversible, on se ramène par des manipulations de colonnes (par la méthode des pivots) à une matrice triangulaire dont les éléments diagonaux sont tous non nuls. A chaque transformation, le déterminant est multiplié par un scalaire non nul. Donc, .
Ainsi,
La valeur absolue du déterminant d'une base a une interprétation géométrique si l'on utilise le produit scalaire naturels de l'espace vectoriel comme volume du parallépipède construit à partir de la base.
Multiplicativité
 0. L'application
0. L'application
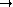 K
K Transposition
On peut ainsi développer le déterminant par rapport à une ligne et les propriétés du théorème-définition restent vraies si on remplace les colonnes par les lignes.
Exercices
- Applications des règles de multilinéarité
- Applications des règles de permutation
- Applications de la multiplicativité
- Produit
- Calcul de déterminant I
- Calcul de déterminant II
- Calcul de déterminant "à la Gauss"
- Déterminant paramétré Déterminant paramétré
Déterminant et vecteurs
- Déterminant et vecteurs
- Produit mixte
- Produit vectoriel
- Produit vectoriel : propriétés
- Aire et déterminant
Aire et déterminant
Il ne reste plus qu'à découper le triangle T en trois triangles et à déformer chacun d'entre eux sans en changer l'aire jusqu'à obtenir une figure remplissant la moitié d'un rectangle de côtés de longueur a et b (et donc d'aire ab) auquel on a enlevé un rectangle de côtés de longueur c et d donc d'aire cd. Magique !
| Plaçons-nous dans le plan contenant les deux vecteurs
v1 et
v2.
L'aire
A à calculer est égale au produit de la longueur
du vecteur
v1
et de la longueur
h de la hauteur
correspondante. Le vecteur
w associé à cette hauteur
est la projection de
v2 sur la droite perpendiculaire à
v1.
Si
w1 = (-b,a) est le vecteur normal à
v1 = (a,b) de même norme, on a donc
|
A =
Déterminant et vecteurs
Soit E un espace vectoriel de dimension n et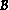 une base.
une base.
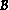 le déterminant
de la matrice des composantes des
vi dans la base
le déterminant
de la matrice des composantes des
vi dans la base 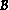 .
On le note
.
.
On le note
.
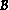 ' est une autre base, si
P est la matrice de passage
de
' est une autre base, si
P est la matrice de passage
de 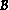 à
à 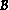 ', on a
', on a
Produit mixte
Considérons un espace vectoriel E de dimension n muni d'un produit scalaire. Choisissons une base orthonormée.
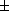 1 .
1 .
Une fois choisie une base orthonormée , le déterminant sépare les bases orthonormées en deux sous-ensembles :
- celles telles que le déterminant de la matrice de passage de est égal à 1 (on les appelle base orthonormée directe)
- celles dont le déterminant de la matrice de passage de est égale à -1 (on les appelle base orthonormée indirecte).
Produit vectoriel
Soit un espace vectoriel E de dimension n muni d'un produit scalaire et d'une base orthonormée .
pour tout vecteur w de E.
Un tel vecteur existe grâce au théorème suivant :
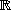 . Alors,
il existe une unique vecteur
a dans
E tel que
.
. Alors,
il existe une unique vecteur
a dans
E tel que
.
Produit vectoriel : propriétés
Les propriétés suivantes se déduisent de la définition et des propriétés du déterminant :
-
Soit
i un entier entre 1 et
n-1. L'application
est linéaire :
-
- est perpendiculaire à chacun des vecteurs vj
- Le calcul des composantes du produit vectoriel de deux vecteurs en dimension 3 est une conséquence de la formule de développement par rapport à la dernière colonne : Si w est de composantes (w1,..., wn) dans la base et si A est la matrice des vecteurs colonnes de v1,...v(n-1) dans la base , on a où la matrice obtenue à partir de A en enlevant la i-ième ligne.
- Si les vecteurs
sont linéairement indépendants,
est non nul et la famille de vecteurs
forment une base directe : le déterminant de ces vecteurs dans la base est strictement positif .