II-1-1 Définitions et Remarques
Définitions
- Soit
b une forme bilinéaire symétrique sur
E.
Deux vecteurs
x et
y de
E sont dits orthogonaux
par rapport à
b si
b(x, y) = 0.
- Une base
(v1,...,vn) de
E est dite orthogonale par rapport à
b si
- Si
q est la forme quadratique associée à
b. Deux vecteurs
x et
y sont
dits orthogonaux par rapport à
q
s'ils sont orthogonaux par rapport à
b.
- Pour tout sous-espace vectoriel
F de
E, on définit
l'orthogonal de
F pour
b , noté
:
Remarques
Soit
une forme bilinéaire symétrique.
- Une base
de
E est orthogonale par rapport à
b si et
seulement si
est diagonale.
- Soit
une base de
E et
, trouver une base orthogonale par rapport à
b revient à trouver
telle que
soit diagonale.
Définition [Vecteur isotrope]
Un vecteur
x est dit
isotrope (pour
q) si
q(
x) = 0.
Remarques
- Il se peut qu'il existe des vecteurs isotropes non nuls. Par exemple, si
et
le vecteur
est isotrope pour
q.
- Les vecteurs du noyau d'une forme quadratique sont isotropes mais la réciproque est fausse.
- Si tout vecteur de
E est isotrope, alors la forme quadratique
q est nulle.
II-1-2 Existence de bases orthogonales
Proposition
Soit
b une forme bilinéaire symétrique de
E, alors
E possède au moins une base orthogonale par rapport à
b.
Démonstration
Montrons ce résultat par récurrence sur
n, la dimension de
E.
La propriété est triviale pour
n=1. Supposons-la vraie pour tout
-espace vectoriel de dimension
n et soient
E un
-espace
vectoriel de dimension finie
n+1 et
b une forme bilinéaire symétrique sur
.
Si
b = 0, alors toute base de
E est orthogonale pour
b et
E admet au moins une base. Supposons donc
.
Si tout vecteur de
E est isotrope, alors
b est nulle.
Donc, il existe
tel que
.
Considérons
et la restriction
b' de
b à
.
Lemme
Soit
e1 un vecteur tel que
, alors
les sous-espaces vectoriels
et
sont supplémentaires
dans
E.
[Démonstration du lemme]
Soit
.
Pour tout
de
, on a
Ceci montre que tout élément
x de
E se décompose d'une
façon unique sur
et
F, donc
et
F sont supplémentaires dans
E.
En particulier,
.
Fin de la démonstration
Revenons à la démonstration de la proposition.
D'après l'hypothèse de récurrence, il existe une base
de
F qui est orthogonale pour
b'. Notons
, on a :
-
est une base de
E car
et
F sont supplémentaires.
-
,
b(e1,ej)=0 car
-
,
Ainsi,
est une base de
E orthogonale pour
b.
Corollaire
Pour toute matrice symétrique
S , il existe une matrice inversible
P et une matrice diagonale
D telle que
Démonstration
Soit
S une matrice symétrique réelle et notons
b la forme bilinéaire symétrique dont la matrice relativement à la base canonique de
est
S. D'après la proposition précédente, il existe une base orthogonale par rapport à
b,
ainsi la matrice de
b dans cette base est diagonale. D'après le théorème de changement de bases pour les formes bilinéaires symétriques, en notant
P la matrice de passage de la base canonique à la base
, on a
.
Fin de la démonstration
Remarque
Attention, les éléments de la diagonale de
D ne sont pas nécessairement les valeurs propres de
S.
Corollaire
Toute forme quadratique
q sur
E est décomposable, d'au moins une façon, en une combinaison linéaire de carrés de formes linéaires indépendantes.
Démonstration
Soient
q une forme quadratique sur
E de forme polaire
b, d'après ce qui précède, il existe une base orthogonale
de
E et la matrice
D de
q dans cette base est diagonale
. Soit
x un vecteur de
E de composantes
dans la base
. L'expression analytique de
q s'écrit alors
En notant
les
sont des formes linéaires, de plus
la famille
est libre car c'est la base duale de
.
Fin de la démonstration
Exemple
Soit
, la forme quadratique définie pour
v = (
x ,
y ,
z) par
Q(v) =
Sa matrice est
A=[].
Une base orthogonale par rapport à
Q est donnée par (v1, v2, v3).
où
v1 = ()
v2 = ()
v3 = ()
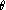 est un polynôme homogène de degré
2 en
.
est un polynôme homogène de degré
2 en
.
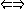 toutes les valeurs propres de
M sont positives.
toutes les valeurs propres de
M sont positives.
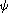 la forme linéaire sur
E
la forme linéaire sur
E
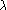 et
et
 de
u.
Dans le repère
, on note
(x', y') les composantes de
M, alors il existe
tel
qu'une équation de
dans
soit
de
u.
Dans le repère
, on note
(x', y') les composantes de
M, alors il existe
tel
qu'une équation de
dans
soit
 ,
on dit que
,
on dit que
 sont
sont